


ответ: ДО=8√3см
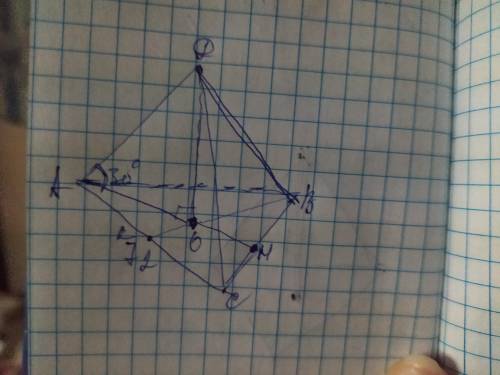
Объяснение: обозначим вершины основания пирамиды А В С, вершину пирамиды Д, а её высоту ДО. В основании правильной трёхугольной пирамиды лежит равносторонний треугольник, поэтому АВ=ВС=АС=72м
Найдём площадь основания по формуле:
S=a²√3/4,где а- сторона основания:
S=72²√3/4=5184//√3/4=1296√3см²
S=1296см².
Проведём из вершин основания медианы АН и ВК. Они пересекаясь в точке О делятся между собой в отношении 2:1, начиная от вершины треугольника: АО: ОН=2:1. Также медиана является ещё и высотой, поскольку треугольник равносторонний. Найдём высоту основания через площадь следуя формуле обратной формуле площади:
S=½×a×h
h=S÷a÷½=1296÷72÷½=18×2=36см
h=36см
Обозначим пропорции 2:1 как 2х и х, и зная величину высоты, составим уравнение:
2х+х=36
3х=36
х=36/3
х=12
ОН=12см, тогда АО=12×2=24см.
Рассмотрим ∆АДО. Он прямоугольный где АО и ДО- катеты, а АД- гипотенуза. Угол ДАО=30°, по условиям, а катет лежащий напротив него равен половине гипотенузы, поэтому ДО=½× АД
Пусть ДО=х, тогда АД=2х, зная, что АО=24см, составим уравнение используя теорему Пифагора:
АД²-ДР²=АО²
(2х)²-х²=24²
4х²-х²=576
3х²=576
х²=576/3
х²=192
х=√192=√(3×64)=8√3
Итак: ДО=8√3см
Объяснение:
1. Найдите площадь треугольника, стороны которого равны 3 см, 7
см и 8 см.
По формуле Герона S=√р(р-а)(р-в)(р-с).
Найдем полупериметр р=(3+7+8):2=9
р-а=9-3=6
р-в=9-7=2
р-с=9-8=1
S=√(9*6*2*1)=6√3.
3. Основа равнобедренного треугольника равна 70 см, а боковая
сторона – 37 см. Найдите радиус круга, описанного вокруг
треугольника.
Центр -лежит вточке пересечения серединных перпендикуляров.
R=(авс)/(4S)
S=1/2*АС*ВН, ВН-высота к основанию АС.
Высота в равнобедренном треугольнике является медианой АН=35см.
ΔАВН-прямоугольный . По т. Пифагора ВН=√(37²-35²)=√(1369-1225)=√144=12(см)
S=1/2*70*12=420 (см²).
R=(авс)/(4S), R=(70*37*37)/(4*420)=1369/24=57 1/24 (см)
Задачи бессмысленные и злые, как взгляд пьяного оберштурмбаннфюрера.
Объяснение:
во вложениях