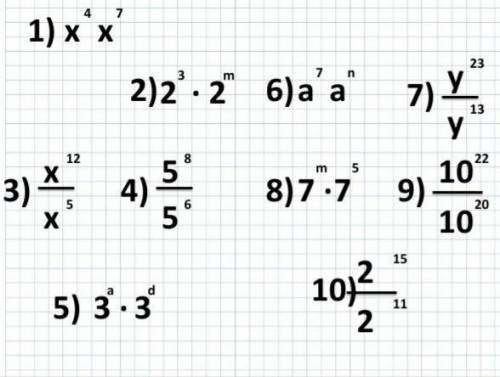
Объяснение:
Чтобы задать функцию нужно найти закономерность (формулу) перехода от координаты х к координате у
1) 1 таблица
1⇒1*3=3
2⇒2*3=6
3⇒3*3=9
4⇒4*3=12
Легко видеть что идет умножение на число 3
тогда функция будет иметь вид y=3x
2) 2 таблица
все значения "у" отличаются от первой таблицы на 1
значит надо просто к "формуле" добавить 1
тогда функия будет иметь вид y=3x+1
3) 3 таблица
все значения "у" отличаются от первой таблицы на 1 (только теперь меньше)
значит надо просто из "формуле" вычесть 1
тогда функия будет иметь вид y=3x-1
4) 4 таблица
все значения "у" отличаются от первой таблицы на "знак"
значит надо просто первую формулу сделать отрицательной
тогда функия будет иметь вид y= -3x
5) 5 таблица
все значения "у" отличаются от четвертой таблицы на 1 (больше)
значит надо просто к 4 "формуле" добавить 1
тогда функия будет иметь вид y= -3x+1
6) 6 таблица
А вот тут линейной закономерности не будет .
Это легко видеть на рисунке (см. приложение)
Вывод: по данной таблице задать функцию нельзя
Если бы в таблице стояли значения
1⇒ -4
2⇒-7
3⇒-10
4⇒-13
То функция имела бы вид у= -3х-1
x = 7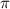
/6
Объяснение:
2 sin x = -1
sin x = -0.5
Отмечаем нужные точки на тригонометрическом круге
Это x = -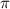
/6 + 2
Так же можно задать это множество решений так:
x =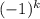
* (-
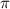/6) +
Нам нужно выбрать из множества решений только те, которые принадлежат заданному промежутку.
Отметим этот промежуток на тригонометрическом круге
Из рисунка видно, что подходит только одно решение x = 7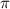
/6
Это решение можно было найти другим решив неравенство
1/2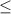
7/6 + 2k
3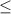
7 + 12k
Так как k - целое, то подходит только k = 0, при других целых k неравенство не выполняется.
1/2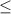
-1/6 + 2k
3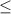
-1 + 12k
Здесь нет целых значений k, для которых бы выполнялось неравенство (при k = 0 -1+0<3, при k = 1 -1+11>9)
Значит, решением является только x = 7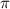
/6
Но здесь проще находить решение именно из тригонометрического круга по рисунку.