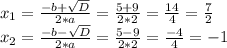
Объяснение:
Предыдущее мое решение было неверным, так как Вы неправильно указали формулировку уравнения.
Если уравнение имеет вид:
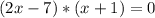
Мы имеем право перемножить обе скобки между собой, получим:
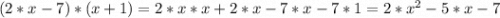
Теперь мы получили обычное квадратное уравнение:
Находим дискриминант:
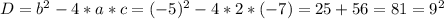
Тогда корни уравнения будут:
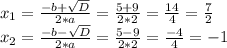
Это и будут корни нашего уравнения.
Можно было решить гораздо проще и приравнять каждую из скобок в произведении уравнения к нулю, и решать как два отдельных уравнения. Тот быстрее, потому что мы без нахождения дискриминанта сразу получаем два корня:
.
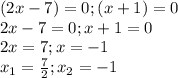
Объяснение:
Нам дан пример:
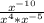
Число в отрицательной степени, это дробь, в которой в числителе будет 1, а в знаменателе наше число, но уже в положительной степени.
Поэтому, разберем сначала знаменатель:
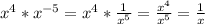- мы преобразовали второе значение переменной согласно правилу выше, и сократили числитель и знаменатель по степени.
Теперь, возвращаясь в исходный пример, получим:
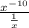
Преобразуем числитель по правилу выше:
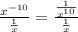
Теперь, по правилу деления одной дроби на другую, вторую дробь мы переворачиваем и умножаем их между собой:
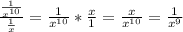- это и будет итоговый ответ на наш пример.
2х+2=0
х=-1