Question

Вычислить cos3α/cosα, если известно, что 2sin3α=sinα

Answer 1

Формулы синуса и косинуса тройного угла:

$\sin3x=3\sin x-4\sin^3x$

$\cos3x=4\cos^3x-3\cos x$

Рассмотрим известное равенство:

$2\sin3\alpha =\sin\alpha$

$2(3\sin\alpha-4\sin^3\alpha ) =\sin\alpha$

$6\sin\alpha-8\sin^3\alpha =\sin\alpha$

$5\sin\alpha-8\sin^3\alpha =0$

$\sin\alpha(5-8\sin^2\alpha) =0$

Возможны две ситуации:

$\sin\alpha=0\Rightarrow \sin^2\alpha=0\Rightarrow \cos^2\alpha =1-\sin^2\alpha=1-0=1$

$5-8\sin^2\alpha =0\Rightarrow \sin^2\alpha =\dfrac{5}{8} \Rightarrow \cos^2\alpha =1-\sin^2\alpha =1-\dfrac{5}{8}=\dfrac{3}{8}$

Рассмотрим искомое выражение:

$\dfrac{\cos3\alpha }{\cos\alpha } =\dfrac{4\cos^3\alpha -3\cos\alpha }{\cos\alpha } =\dfrac{\cos\alpha(4\cos^2\alpha -3) }{\cos\alpha } =4\cos^2\alpha -3$

Зная два возможных значения квадрата косинуса, найдем возможные значения выражения.

При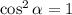 $\cos^2\alpha =1$:

$\dfrac{\cos3\alpha }{\cos\alpha } =4\cdot1 -3=1$

При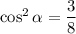 $\cos^2\alpha =\dfrac{3}{8}$:

$\dfrac{\cos3\alpha }{\cos\alpha } =4\cdot\dfrac{3}{8} -3=\dfrac{3}{2} -3=-\dfrac{3}{2}=-1.5$

ответ: 1 или -1.5