
Объяснение:
у нас по условию есть точки
А(5;8)
В(0; у) - лежит на оси оу
С(1; -4)
из того, что это ромб, мы понимаем, что стороны АВ = ВС
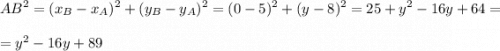
аналогично считаем ВС

и теперь
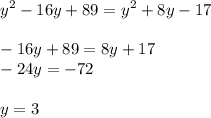
мы нашли координаты точки В(0;3)
теперь мы можем провести прямую через точки A(5;8) и В(0;3)
мы будем проводить и ещё прямые. я здесь распишу подробно как найти уравнение прямой, проходящей через две точки. дальше буду вывод уравнения опускать. писать только само уравнение
итак, прямая через точки А(5;8) и В(0;3)

мы получили каноническое уравнение прямой
из него легко получить уравнение прямой с угловым коэффициентом:
y = x + 3
теперь мы знаем, что поскольку это ромб, то АВ║CD
тогда уравнение прямой CD (через точки С и D) имеет тот же коэффициент угла наклона (коэффициент при х), что и прямая АВ, т.е. это уравнение вида
у=x+b
и эта прямая проходит через точку С(1; -4), значит координаты точки С должны удовлетворять уравнению прямой. подставим координаты точки С в уравнение
-4 = 1+b ⇒ b = -5
и тогда мы имеем уравнение прямой CD
у = х - 5
аналогично найдем уравнение прямой АD
сначала уравнение прямой ВС (по двум точкам)
у = -7х +3
а потом уравнение ║ ей прямой AD
y = -7x +b она проходит через точку А
8 = (-7)*5+ b b = 43
уравнение прямой AD
y = -7x + 43
теперь мы можем найти координаты точки D как пересечение прямых ВС и CD
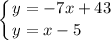
x - 5 = -7x +43
8x = 48
x = 6; y = 1
мы нашли координаты точки D(6; 1)
итак, наши точки
А(5;8)
В(0; 3)
С(1;4)
D(6; 1)
теперь уравнение диагонали BD
уравнение прямой, проходящей через две точки

или
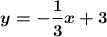
ответ
уравнение диагонали BD 
точка В(0; 3)
точка D(6; 1)
на графике изображены все прямые и все точки
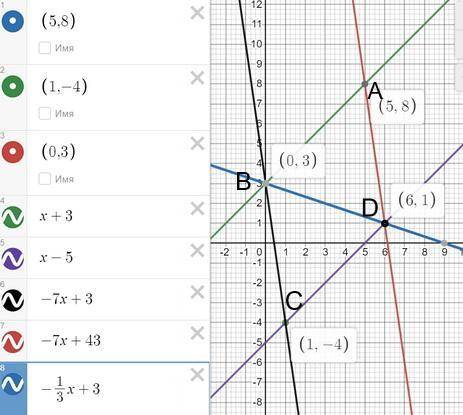
Т.к отношение площадей треугольников равно квадрату коэффициента подобия, то к=3,а SАОD /SВОС=3^2, т.е 9.
Объяснение:
f(х)=1/3х³+х²-3х+5/3=1/3(х-1)(х+5)
Функция не является ни четной ни нечетной
2, D(f(х)): (-∞;+∞)
Точки пересечения с осями координат
С осью (Ох) А(-5;0) В(1;0)
С осью (Оу) С(0; 5/3)
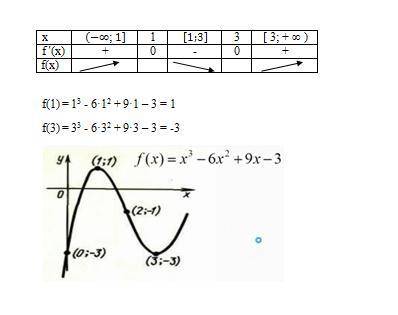
3. Точки экстремума
Определяем когда f(х) '=0
(1/3х³+х²-3х+5/3)'=0 х²+2х-3=0 Д= D=22- 4·1·(-3)=16
Корни уравнения:
х₁=(-2+4)/(2*1)=1
х₂=(-2-4)/(2*1)=-3
х₁=1 у₁=0
х₂=-3 у₂=10²/₃
4. f(х) возрастает при х∈(-∞;-3)
Убывает х∈(-3;1)
возрастает при х∈(1;+∞)
сводим все в таблицу
х (-∞;-3) -3 (-3;1) 1 (1;+∞)
f(х) ' + 0 - 0 +
f(х) ↑ 10²/₃ ↓ 0 ↑