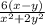ответ: 1 -------------------------------------- если коэффициенты действительно такие, то это уравнение решается лишь за формулами Кардано (на подобие формул корней квадратного уравнения, только для уравнения 4-го степени). И тут не применишь и метод неопределенных коэффициентов (ax^2+bx+c)(dx^2+ex+f)=5x^4-12x^3+11x^2-12x+5, так как коэффициенты b,c,e,f - иррациональны. Формулы Кардано в обычном курсе алгебры в школе не изучают, в углубленном курсе кажется так же не изучают. Прикрепляю скрин
, , , , ,
два случая: 1)
2)
ответ: 1 и 5 ------------------------------ - парабола ветками вверх, нам нужен случай, когда вершина параболы лежит на оси ОХ, т.е. когда парабола пересекает эту ось в одной точке. И это будет тогда и только тогда, когда дискриминант обращается в нуль: Получили, что это случается если
см ниже, проверь правильность записи условий 2) и 5)
Обьяснение:
1)с/с+3 - с/с-2=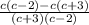 =
=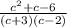
2)5/6m+6 - 3/2m2 =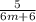 -
-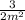 =
=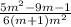
3)a/a-в - a^2/a^2-в^2 =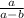 -
- 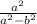 =
= 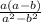 -
- 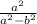 =
= 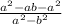 = -
= -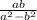
4)2+ x/y+ y/x = 2+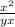 +
+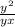 =2+
=2+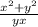
5)3x+1/3x- 2y+1/2y + 3x-y/6xy =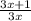 +
+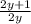 +
+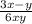 =
=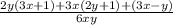 =
=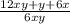
6)y^2/y^2-2y+1 - y/y-1 =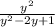 =
=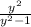
7)3/x+2y + 3x/x^2+4xy+4y^2 =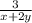 +
+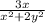 =
=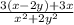 =
=