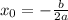
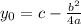 (ещё игрек можно вычислить, подставив икс в нашу квадратичную функцию)
(ещё игрек можно вычислить, подставив икс в нашу квадратичную функцию)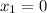
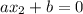
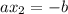
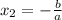
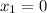 и
и 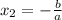 . Теперь найдём среднее арифметическое этих двух чисел, чтобы вычислить координату x точки, находящейся посередине, через которую проходит ось симметрии параболы (это и будет координата
. Теперь найдём среднее арифметическое этих двух чисел, чтобы вычислить координату x точки, находящейся посередине, через которую проходит ось симметрии параболы (это и будет координата 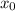 вершины параболы):
вершины параболы):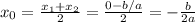
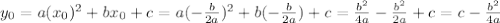
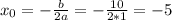
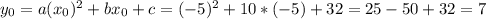
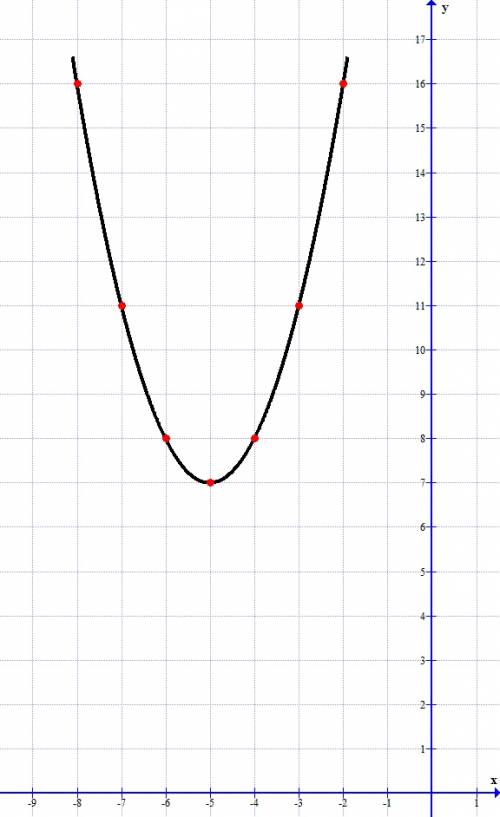
Выделим все три коэфф. данного трёхчлена: 8x2 - 3bx + 18.
Полным квадратом является трёхчлен такого вида a2x2 ± 2acx + c2.
Выразим коэффициент при x через два других: при x2и свободный член:
Т.к. b>0, то 3b = 2?8·?18, отсюда 3b = 24, получаем b = 8.
Чтобы квадратный трёхчлен был полным квадратом,
его дискриминант должен быть равен нулю: D = (3b)2- 4·8·18 = 0.
Решим уравнение: 9b2 - 576 = 0, получим b2 = 64, отсюда b = ±8.
Учитывая, что b>0, получаем окончательно b = 8.