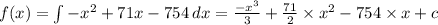
Скорость котёнка = 110 м/ мин, а скорость щенка = 100 м/мин
Объяснение:
1) Т.к. ответы просят в метрах в минуту, то надо перевести всё в эти единицы
20 секунд = 1/3 минуты
60 секунд = 1 минута
2) Составим систему
Скорость = Расстояние : время
Первое уравнение это будет наша скорость удаления. Тут мы скорости складываем
Второе уравнение - скорость сближения. Здесь вычитаем из большей меньшую скорость (Т.к. котёнок обогнал щенка, значит его скорость больше)
Пусть скорость котёнка - х, а скорость щенка - у, тогда
⁺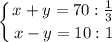
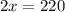
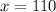 м/мин - скорость котёнка
м/мин - скорость котёнка
Подставим это значение в одно из уравнений
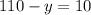
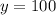 м/мин - скорость щенка
м/мин - скорость щенка
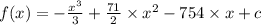
Объяснение:
Предположим что производственной функции является квадратное уравнение.
Знаем что экстремум функции это когда производная этой функции равна нулю.
1) Зная корни производной (13 и 58) запишем его и проверим возрастание и убывание функции:
f'(x) = (x-13)*(x-58)
f'(0)=(0-13)*(0-58)=754
f'(14)=(14-13)*(14-58)=-44
Данные условия не соблюдаются. Так как 13 является максимум, а 58 минимум функции.
Умножим производную на - 1.
2)
f'(x) = -1*(x-13)*(x-58)
f'(0)= - 1*(0-13)*(0-58)=-754
f'(14)= - 1*(14-13)*(14-58)=44
Условия соблюдаются.
3) Найдем первообразную функции
f'(x) = -1*(x-13)*(x-58)=-x^2+71*x-754