
Так как квадраты чисел неотрицательны, то х²≥0 при любых значениях х.Наименьшее значение , которое принимает х² равно нулю, а наибольшего не существует, так как значение х² может только увеличиваться. То есть 0≤х²<+∞. А теперь от этого неравенства, от всех его частей отнимем 5, получим 0-5≤х²-5<∞-5. Получим -5≤х²-5<∞. От бесконечности какое не отнимай постоянное число ( или прибавляй к ней) она всё равно останется БЕСКОНЕЧНОСТЬЮ.
Можно было нарисовать график у=х²-5. Это парабола с вершиной в точке (0,-5), ветви вверх. Мысленно ( или не мысленно, а явно) спроектируй все точки, лежащие на параболе на ось ОУ.Увидишь, что все у-ки попадут в промежуток [0,∞), то есть у∈ [0,∞).
Пусть х км/ч - скорость, с которой Иван ехал на велосипеде, тогда x+30 км/ч - скорость, с которой Иван ехал на автомобиле. На велосипеде Иван проехал 24 км, а на автомобиле 84 км за это же время.
24/x ч - время, за которое Иван проехал 24 км на велосипеде.
84/(x+30) ч - время, за которое Иван проехал 84 км на автомобиле.
Составим уравнение (помним, что время одинаковое):
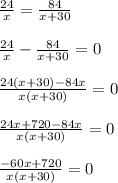
ОДЗ: x≠0; x≠-30 (т.к. на 0 делить нельзя)
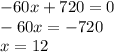
12 км/ч - скорость, с которой Иван ехал на велосипеде.
24/12=2 ч - за это время Иван проехал 24 км на велосипеде.
А т.к. время равно, что за первое расстояние, что за второе расстояние, то и за 2 ч Иван проехал 84 км на автомобиле.
ответ: 12 км/ч; 2 ч

S заштрихованной фигуры = 1