Объяснение:
1) Приводишь к общему знаменателю и при этом выполняется:
6х - 1 ≠ 0
х ≠ 1/6
(x+2)(6x-1) = 15
6x^2-x+12x-2-15 = 0
6x^2+11x-17 = 0
D = b^2-4ac
D = 11^2-4*6*(-17) = 121+408 = 529
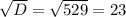
x1 = (-b+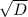
)/2a = (-11+23)/2*6 = 12/12 = 1
x2 = (-b-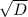)/2a = (-11-23)/2*6 = -34/12 = -17/6
ответ: 1; -17/6
2) Чтобы найти точку пересечения двух графиков достаточно их приравнять и решить уравнение, т.е.:
2/x = x-1
2/x - x + 1 = 0
-x^2+x+2 = 0 Домножим на (-1):
x^2 -x -2 =0
по т. Виета:
x1+x2 = 1
x1*x2 = -2
x1= 2 x2= -1
Если x = 2, то у = 1
Если х = -1, то у = -2
ответ: (2;1) и (-1;-2)
10, 50 и 30 минут
Объяснение:
1 встреча:
старт улитки с отметки "15 минут", т. е. с числа 3, а старт минутной стрелки в 15:00, т. е. с числа 12. Расстояние между этими числами 15 промежутков. t=S/V t=15/1,5=10 (минут) – произойдёт первая встреча после старта. Минутная стрелка будет на числе 2, а это отметка "10 минут".
2 встреча:
Улитка будет двигаться против часовой стрелки и встретиться с минутной через 60/1,5=40 минут, а минутная стрелка в этот момент будет на отметке 10+40=50минут.
3 встреча:
Потом встреча состоится ещё через 40 минут, когда минутная стрелка будет находиться на отметке 30 минут, т.е. от отметки 50 минут(на часах это число 10) до 1 часа (число 12) пройдет 10 минут и + ещё 30 минут (число 6).