1. Решим первое неравенство этой системы:
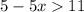
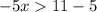
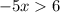
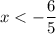
ответ: 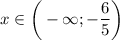
2. Дробь 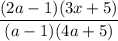 существует, если
существует, если
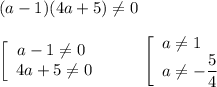
Перед тем как выражать  , нужно рассмотреть случаи, когда дробь
, нужно рассмотреть случаи, когда дробь 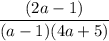 положительная, а когда отрицательная:
положительная, а когда отрицательная:
 знак неравенства меняться не будет (так как делим (умножаем) на положительное число):
знак неравенства меняться не будет (так как делим (умножаем) на положительное число):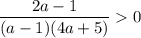
Решим неравенство методом интервалов.
а) ОДЗ: 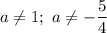
б) Нуль неравенства: 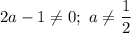
в) Решением данного неравенства будет 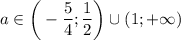 .
.
При таких значениях параметра  знак неравенства меняться не будет:
знак неравенства меняться не будет:
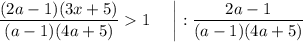
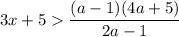
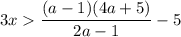
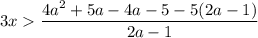
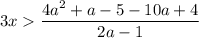
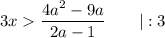
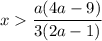
 знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):
знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):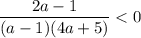
Решим неравенство методом интервалов. Решением данного неравенства будет  .
.
При таких значениях параметра  знак неравенства изменится:
знак неравенства изменится:
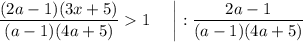
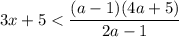
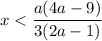
ответ: если  , то
, то 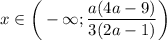 ; если
; если 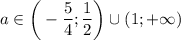 , то
, то 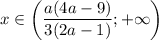 ; если
; если 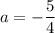 и
и 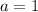 , то неравенство не имеет решений.
, то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра  , поэтому:
, поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если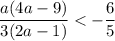 , то есть
, то есть 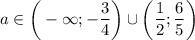 , то в объединении с
, то в объединении с 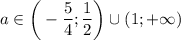 получаем
получаем 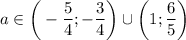
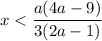 при
при  Если
Если 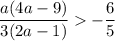 , то есть
, то есть 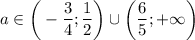 , то в объединении с
, то в объединении с  получаем, что таких
получаем, что таких  не существует, то есть такого варианта эта система не имеет.
не существует, то есть такого варианта эта система не имеет.2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png)
ответ: если  , то
, то 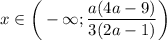 ; если
; если 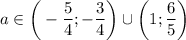 , то
, то 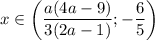 ; если
; если ![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png) , то система не имеет решений.
, то система не имеет решений.
ответ: Можно.
Объяснение:
Разделим квадрат на 144 равнобедренных треугольника. ( Сначала на 36 квадратов, потом каждый квадрат двумя диагоналями на четыре равнобедренных треугольника.)
Минимально квадрат можно сложить из двух или четырех равнобедренных треугольников.
Нужны числа из которых можно извлечь корень и которые кратны 4.
Это: 4; 16; 36; 64; 100. ( для квадратов состоящих из 4 частей )
И удвоенное произведение этих чисел включая 1.
Это: 2; 8; 32; 72; 128. ( для квадратов состоящих из 2 частей )
Зная, что сумма трёх чисел равна 144, найдем количество частей в каждом из трёх квадратов. (количество частей для каждого квадрата должно быть разное)
К примеру:
100+36+8=144
1 кв. из 100 частей ; 2 кв. из 36 частей; 3 кв. из 8 частей.
Или
64+72+8=144
1 кв. из 64 частей ; 2 кв. из 72 частей; 3 кв. из 8 частей.
Рисунок смотрите на фото.