Объяснение:
Для начала найдем область определения функции, и ее потенциальные точки разрыва
1)D(f)=R, точек разрыва нет
2) проверим функцию на четность, очевидно функция четная, т.к. при подстановке вместо икс минус икс функция вида не изменит.
3) найдем нули функции и знак функции на полученных интервалах, для этого разложим функцию на составляющие x^4-1=(x^2-1)(x^2+1)=(x-1)(x+1)(x^2+1)
Приравняем это к нулю, тогда x=1 x=-1
Исследуем знак функции на промежутках от минус бесконечности до минус 1, от минус 1 до 1, и от 1 до +бесконечности. Для этого подставим любую точку из промежутков и получим знаки +-+ (значит на промежутке от -беск до -1 и от 1 до+беск, функция выше оси Ох, на промежутке -1 до 1 функция ниже оси Ох)
приравняв к нулю икс, получим игрик равный -1
4)найдем ассимптоты, так как точек разрыва нет, то и вертикальных ассимптот нет, найдем наклонную асимптоту, для этого вычислим предел
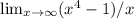 стремится к бесконечности, а значит ассимптот нет
стремится к бесконечности, а значит ассимптот нет
5)Исследуем точки экстремума и интервалы монотонности, тогда найдем производную
4x³ и приравняем ее к нулю 4x³=0, откуда x=0. Найдем знаки слева и справа от нуля, слева минус справа плюс, значит слева от нуля функция убывает, а справа возрастает. Т.к. 0 принадлежит области определения функция, то подставим его в изначальное уравнение, получим -1. Точка (0,-1) - точка экстремума, т.к. в этой точке производная меняет знак с минуса на плюс, то это точка минимума
6) найдем точки перегиба. Для этого найдем вторую производную - производную от производной = 12x^2. приравняем к нулю и вновь получим 0, найдем знаки слева и справа, с обеих сторон +, значит функция выпукла вниз на всей области определения, и точка 0 не является точкой перегиба
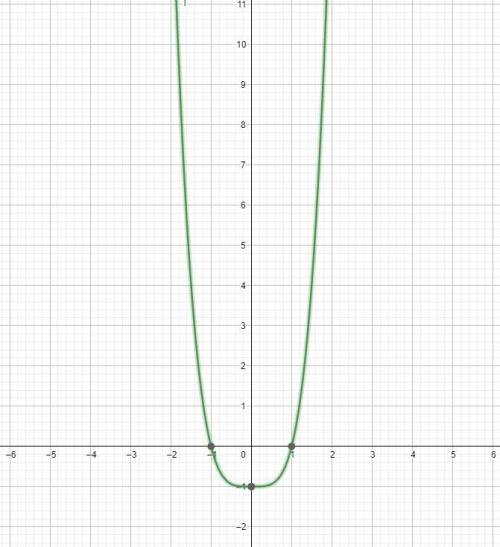
7) нужно построить график по всем значениям которые мы получили
Дано, что катер за 2 часа по течению и 3 часа против течения 150 км;
за 4 часа по течению на 12 км меньше, чем за 6 часов против течения.
Найти собственную скорость катера.
Решение. Пусть x — расстояние, пройденное за 1 час по течению, y — расстояние, пройденное за 1 час против течения.
Составим систему уравнений:
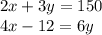
Решим её, методом подстановки, например:
2x + 3y = 150
2x = 150 – 3y
2*(150 – 3y) – 12 = 6y
300 – 6y – 12 = 6y
-12y = -288
y = 24 ___
2x + 3*24 = 150
2x = 78
x = 39 ___
Получается, U по течению = 39 км/час, U против течения = 24 км/час.
Формула нахождения собственной скорости:
U собств. = (U по теч. + U против теч.) / 2
U собств. = (39+24)/2 = 31.5 км/час
ответ: 31.5 км/час
1)x=±1; (тут просто выносим 4 и выходит 4*(x^2-1)=0, ну а равняется уравнение 0 когда один из множителей равняется 0)
2) x=-19/8; 1 (тут просто по дискриминанту)
3) x ничему не равняется еле же x=±6i (число в квадрате не может быть меньше нуля, ну а если решать на комплексных числах то x=±6i)
4) x=-4; x=-1 (по теореме Виета, еле по дискриминанту)
5) x=4 (можно сгрупировать еле по дискриминанту)
6) x=1/5; x=2 (по дискриминанту)
7) x=1/5; x=4 (по дискриминанту)
8) x ничему не равняется еле же x=(3±i√191)/20 (тут дискриминант меньше нуля будет, поэтому если решение и есть то оно на площади комплексных чисел)
9) x=-7; x=0; (выносим x и выходит x*(x+7)=0, ну а равняется уравнение 0 когда один из множителей равняется 0)
10)x=±0.5; (тут просто выносим 64 и выходит 64*(1/4-t^2)=0, ну а равняется уравнение 0 когда один из множителей равняется 0)
11) x=1; x=5/3; (по дискриминанту)
12) x ничему не равняется еле же x=±i*√15 ( можно вынести минус и тогда выйдет -(15+x^2)=0 число в квадрате не может быть меньше нуля, ну а если решать на комплексных числах то x=±i*√15)
13) x=-1; x=4/5 (по дискриминанту)
14) x=-6; x=5 (по теореме Виета, еле по дискриминанту)
15) x=2/3; (по дискриминанту)
16) y=2/5; y=1/2 (по дискриминанту)
17) x=6/5; x=2 (по дискриминанту)
18) x ничему не равняется еле же x=( -1±i*√(19) )/10 ( Дискриминант меньше нуля соответственно решение есть только на комплексных числах то x=( -1±i*√(19) )/10;
19) x=0; x=0.5 (тут просто выносим 4x и выходит 4x*(0.5-x)=0, ну а равняется уравнение 0 когда один из множителей равняется 0)