-64 + а⁶
Объяснение:
(-4+а²)(16+а⁴+4а²)= -4(16+а⁴+4а²) + а²(16+а⁴+4а²)= -64 -4а⁴-16а²+16а²+а⁶+4а⁴= -64+а⁶
12 км/час
Объяснение:
Моторная лодка за 8 часов проплыла 45 км против течения и вернулась обратно. Найди скорость моторной лодки в стоячей воде, если скорость течения реки равна 3 км/час.
Скорость моторной лодки в стоячей воде v км/час
Скорость моторной лодки против течения (v-3) км/час
Скорость моторной лодки по течению (v+3) км/час
Время затраченное на путь против течения 45/(x-3) час
Время затраченное на путь по течению 45/(x+3) час
45/(x-3)+45/(x+3)=8
(x-3)(x+3)(45/(x-3)+45/(x+3))=8(x-3)(x+3)
45(x+3)+45(x-3)=8(x²-9)
45x+135+45x-135=8x²-72
8x²-90x-72=0
4x²-45x-36=0
D=2025+576=2601=51²
x₁=(45-51)/8=-3/4<0
x₂=(45+51)/8=12 км/час
4+0+...4(2-n)=2n(3-n)
Док-во: 1) Проверим, что верно n=1: 4=2*1(3-1); 4=2(2); 4=4 -верно
2)Допустим, что верно для n=k, тогда: 4+...+4(2-k)=2k(3-k)
3)Докажем, что верно для n=k+1, тогда 4+...+4(2-(k+1))=2(k+1)(3-(k+1));
4+...+4(2-1-k)=2(k+1)(3-1-k); 4+...+4(1-k)=2(k+1)(2-k) -?
4+...+4(1-k)=2(k+1)(2-k)=> {4+...+4(2-k)}+4(1-k)= то, что находится в {...} заменяем на то, что получили во втором шаге, т.е. на 2k(3-k), получаем
= 2k(3-k)+4(1-k)=6k-2k^2+4-4k= 6k-4k-2k^2+4= 2k-2k^2+4= -(2k^2-2k-4)
Раскладываем квадратное уравнение -(2k^2-2k-4)=0; D=4+32=36=6^2
k1=(2-6)/4=-4/4=-1; k2=(2+6)/4=10/4 => -(2k^2-2k-4)=-2(k-10/4)(k+1)=(-2k+5)(k+1)=
=(5-2k)(k+1)=2(2.5-k)(k+1)
Получается, что неверно, но м.б. я гдн-то ошибся, но в общем такого вида получается док-во
Применим формулу разности кубов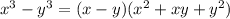 .
.