Произведите умножение: а) (a - b)(a+b)(a + b2);
в) (m2 +b)(m - b)(m6 +b2);
б) (2x +y)(4х2 +y2)( 2х - у);
г) (а? + 1)(a - 1)(а+ 1)

👇

Увидеть ответ

Ответ:

770glym

07.04.2022

а) (a - b)(a+b)(a² + b²)=(a² - b²)(a² + b²) =a⁴ - b⁴ ;

в) (m² +b)(m² - b)(m⁴ +b²) = (m⁴ - b²)(m⁴ +b²)= m⁸- b⁴ ;

б) (2x +y)(4х² +y²)( 2х - у)= (2x +y)( 2х - у) (4х² +y²)=

=(4х² -y²)(4х² +y²)=16x⁴-y⁴ ;

г) (а² + 1)(a - 1)(а+ 1)= (а² + 1)(a² - 1²)=a⁴-1

4,8(82 оценок)

Открыть все ответы

Ответ:

Katya111zz3

07.04.2022

Объяснение:

a) нет (любое отрицательное целое число не является натуральным, например -1)

б) да

в)нет ( например число 1,25)

г)Нет (например число √7 будет действительным и иррациональным)

3) 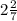$2\frac{2}{7}$ = 16/7 = 160/70

2,2 = 22/10 = 144/70, значит 16/7>2,2

2,3 = 23/10 = 161/70, значит 16/7<2,3 , а значит правильный ответ 2 ( не знаю почему учитель поставил -, наверное ошибся)

ответ: 2

4) Площадь прямоугольника находится по формул S = a*b, где a и b его стороны

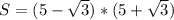$S=(5-\sqrt{3})*(5+\sqrt{3} )$ тут мы видим разность квадратов

S = 5²-√3² = 25 -3 = 22

ответ : 22

5) $4\sqrt{2} = \sqrt{16*2} = \sqrt{32} \\5 = \sqrt{25} \\6 = \sqrt{36}$

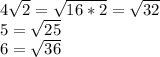
$\sqrt{25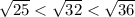}$ , значит 4√2 находится между ними

середина между 25 и 36 - число 31, а т.к 32>31, то точка будет ближе к числу 6, а значит ответ 3)P

ответ: 3

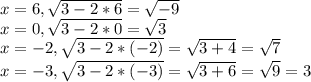
$x = 6, \sqrt{3 - 2*6} = \sqrt{-9} \\x = 0, \sqrt{3 - 2 *0} =\sqrt{3} \\x = -2, \sqrt{3-2*(-2)} =\sqrt{3+4} = \sqrt{7} \\x = -3, \sqrt{3 - 2 *(-3)} =\sqrt{3+6} = \sqrt{9} = 3$

В 1 случае нет решения, т.к корень отрицательный

Во 2 и 3 корни иррациональные

В 4 уравнение мы получили число 3 - рациональное, значит ответ 4

ответ: 4

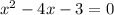
$x^{2} -4x -3 = 0$

D= (-4)²-4*1*(-3) = 16 + 12 =28

$x(1) = \frac{4+\sqrt{28} }{2} = \frac{4+2\sqrt{7} }{2} = \frac{2(2+\sqrt{7}) }{2} = 2+\sqrt{7}$

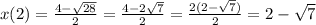$x(2) = \frac{4-\sqrt{28} }{2} = \frac{4-2\sqrt{7} }{2} = \frac{2(2-\sqrt{7}) }{2} = 2-\sqrt{7}$ - подходит

б)5x²-x = 0

x(5x-1)=0

x = 0 или 5x -1 = 0

5x = 1

x = 0,2 - не подходит, т.к тут корни уравнения рациональные

в) 1 - 4x²= 0

4x² = 1

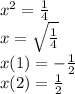$x^{2} =\frac{1}{4}\\x = \sqrt{\frac{1}{4} } \\x(1) = -\frac{1}{2} \\x(2) =\frac{1}{2}$ - не подходит, т.к тут рациональные корни уравнения

ответ: 1

8) тут просто подставляем x и y

M: 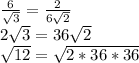$\frac{6}{\sqrt{3} } = \frac{2}{6\sqrt{2} } \\2\sqrt{3} = 36\sqrt{2} \\\sqrt{12} =\sqrt{2*36*36}$ - неверно

N: 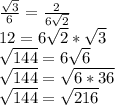$\frac{\sqrt{3} }{6} =\frac{2}{6\sqrt{2} } \\12 = 6\sqrt{2} *\sqrt{3} \\\sqrt{144}= 6\sqrt{6}\\\sqrt{144} = \sqrt{6*36} \\\sqrt{144}=\sqrt{216}$ - неверно

P: 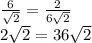$\frac{6}{\sqrt{2} } =\frac{2}{6\sqrt{2} } \\2\sqrt{2} = 36\sqrt{2}$ - неверно

ну методом исключения правильный ответ 4) Q , но лучше перепроверить

Q: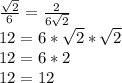 $\frac{\sqrt{2} }{6} =\frac{2}{6\sqrt{2} } \\12 = 6*\sqrt{2} *\sqrt{2} \\12 = 6 *2\\12 = 12$ - истина

ответ: 4

4,7(15 оценок)

Ответ:

martynenko7474

07.04.2022

1)х∈ (-∞, -5)∪(3, +∞).

2)Решение системы уравнений (4; 3); (3; 4).

3)Согласно графика, координаты точек пересечения (-1;2); (1; 2).

Объяснение:

1)Найти область определения:

а)по ОДЗ х≠5;

б)подкоренное выражение должно быть всегда больше либо =нулю:

х²+2х-15>=0

Приравнять к нулю и решить как квадратное уравнение:

х²+2х-15=0

D=b²-4ac = 4+60=64 √D= 8

х₁=(-b-√D)/2a

х₁=(-2-8)/2

х₁= -10/2

х₁= -5;

х₂=(-b+√D)/2a

х₂=(-2+8)/2

х₂=6/2

х₂=3.

Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -5 и х=3, отмечаем эти точки схематично, смотрим на график.

По графику ясно видно, что у>=0 (как в неравенстве), слева и справа от значений х, то есть, область определения функции в интервале

х∈ (-∞, -5)∪(3, +∞).

2)Решить систему уравнений:

ху=12

2х+2у-ху=2

Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:

х=12/у

2(12/у)+2у-12-2=0

24/у+2у-14=0

Умножить уравнение на у, чтобы избавиться от дроби:

24+2у²-14у=0

Разделить уравнение на 2 для упрощения: