0,5х-2у=0 х-у-3=0
0,5х=2у у=х-3
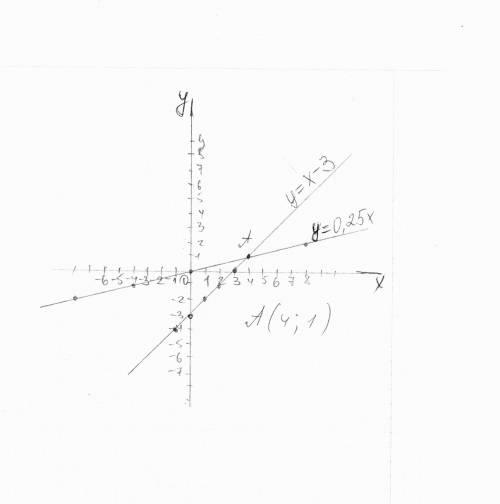
у=0,25х
Теперь подставляем вместо х любое число,находим у и строим графики.Например:
0,25*0=0 (х=0,у=0)
0,25*4=1 (х=4,у=1) и т.д.
Так же и со вторым уравнением:
0-3=-3 (х=0,у=-3)
5-3=2 (х=5,у=2) и т.д.
Когда построите эти графики,они пересекуться в точке(4;1).Можно доказать это и по другому.Приравняем правые части наших уравнений:
0,25х=х-3
х-0,25х=3
0,75х=3
х=4
Подставим это значение в наши уравнения и найдем у:
0,25*4=1 и 4-4=1, т.е. у в обоих случаях=1
ответ: (4;1)
По теореме Виета для уравнения вида:
х² + px + c = 0
Можно подобрать такие корни, что:
x1*x2 = c
x1+x2 = –p
Я обычно подбираю числа, дающие при умножении в уравнении число 'с', с таблицы умножения, а потом расставляю знаки так, чтобы получить '–р' (число возле 'х' с противоположным знаком). Таким образом, уравнения по т. Виета решаются устно (методом подбора).
а) х² + 11х + 28 = 0
х1 = -7; х2 = -4 (по т. Виета)
Действительно:
х1*х2 = -7*(-4) = -28 (это 'с)
х1+х2 = -7+(-4) = -11 (это '-р')
ответ: -7; -4
б) х² - 12х + 27 = 0
х1 = 3; х2 = 9 (по т. Виета)
Действительно:
х1*х2 = 3*9 = 27 (это 'с')
х1+х2 = 3+9 = 12 (это '-р')
ответ: 3; 9
в) х² + 37х + 36 = 0
х1 = -36; х2 = -1 (по т. Виета)
Действительно:
х1*х2 = -36*(-1) = 36 (это 'с')
х1+х2 = -36-1 = -17 (это '-р')
ответ: -36; -1
г) х² - 16х - 36 = 0
х1 = -2; х2 = 18 (по т. Виета)
Действительно:
х1*х2 = -2*18 = -36 (это 'с')
х1+х2 = -2+18 = 16 (это '-р')
ответ: -2; 18
Первое, второе и пятое являются ошибочными.
Так как в первом 2 десятые больше чем сотые, во втором 6 целых и 68 целых, в пятом опять же, сотые меньше чем десятые.