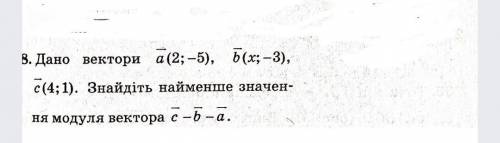
Объяснение:
Для каких из уравнений пара чисел (6;-1.5) является решением уравнения?
1) x+y=4,5
6-1,5=4,5 да
2)2x+4y-15,4=2,6
2*6+4*(-1,5)-15,4=
=12-6-15,4= -9,4
-9,4≠2,6 нет
3)1,3x(12-4x)+5y=101,1
1,3*6(12-4*6)+5*(-1,5)=
=7,8(12-24)-7,5=
=7,8*(-12)-7,5=
= -93,6-7,5= -101,1
-101,1≠101,1 нет
4)-2,1x=8,4y
-2,1*6=8,4*(-1,5)
-12,6= -12,6 да
5)x^2-xy=45
6²-6*(-1,5)=
=36+9=45
45=45 да
6)-3,8x(5,1x-3,4y)= -96,9
-3,8*6(5,1*6-3,4*(-1,5)=
= -22,8(30,6+5,1)=
=-22,8*35,7= -813,96
-813,96≠ -96,9 нет
7)x-3x+5y=7,5
6-18-7,5= -19,5
-19,5≠ 7,5 нет
а(2;-5) б(х;-3) с(4;1)
координаты вектора a-b-c( 2-x-4 ; -5+3-1)
a-b-c( -2-x ; -3)
| a-b-c|=√(-2-x)²+(-3)²)=√(4+4x+x²+9)=√(x²+4x+13) наименьшее значение парабола у=x²+4x+13 принимает в вершине
х₀=(-4)/2=-2
ответ -2