Відповідь:
1. Начинать закаливающие процедуры необходимо только когда человек полностью здоров.
2. Обязательно соблюдать принцип постепенности. В начале применения закаливающих процедур у организма возникает определенная ответная реакция со стороны дыхательной, сердечно- сосудистой и центральной нервной систем. По мере неоднократного повторения этой процедуры реакция на нее организма постепенно ослабевает, а дальнейшее ее использование уже не оказывает закаливающего эффекта. Тогда надо изменить силу и длительность воздействия закаливающих процедур на организм.
3. Очень важно проводить закаливающие процедуры регулярно и без больших перерывов. Следует помнить, что проведение закаливающих процедур в течение 2-3 месяцев, а затем их прекращение приводит к тому, что закаленность организма исчезает через 3-4 недели, а у детей через 5-7 дней. В случае появления признаков заболевания закаливание временно прекращают, после выздоровления следует возобновить его с начального периода.
Пояснення:
1. Начинать закаливающие процедуры необходимо только когда человек полностью здоров.
2. Обязательно соблюдать принцип постепенности. В начале применения закаливающих процедур у организма возникает определенная ответная реакция со стороны дыхательной, сердечно- сосудистой и центральной нервной систем. По мере неоднократного повторения этой процедуры реакция на нее организма постепенно ослабевает, а дальнейшее ее использование уже не оказывает закаливающего эффекта. Тогда надо изменить силу и длительность воздействия закаливающих процедур на организм.
3. Очень важно проводить закаливающие процедуры регулярно и без больших перерывов. Следует помнить, что проведение закаливающих процедур в течение 2-3 месяцев, а затем их прекращение приводит к тому, что закаленность организма исчезает через 3-4 недели, а у детей через 5-7 дней. В случае появления признаков заболевания закаливание временно прекращают, после выздоровления следует возобновить его с начального периода.
Биквадратное уравнение.
Решается заменой переменной:

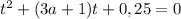
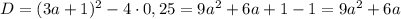
Если D >0, т.е.


уравнение имеет корни:
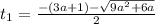 или
или 
Обратный переход:
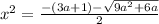 или
или 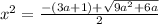
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
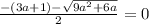
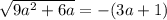
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
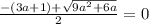
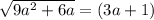
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 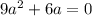
 или
или 
При 
уравнение принимает вид:

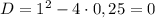 ⇒
⇒ 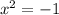
уравнение не имеет корней
При 
уравнение принимает вид:

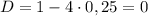 ⇒
⇒ 
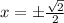
Уравнение 4-ой степени, значит
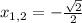 и
и 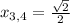
О т в е т. При 
f'(x) = 3x² +24x²+2(24-3x)*(-3) = 27x²+18x-144=27(х-2)(х+2/3)
27x²+18x-144=0
3x²+2x-16=0
x=2, x=-2/3.
При переходе через точку 2 знак производной меняется с минуса на плюс,х=2 - точка минимума.
ответ: первое число 2, второе - 4, третье - 18.