Решать надо методом интервалов, для этого надо найти нули функции , решим для уравнение
Получаем разложение
Там интервалы были, знаки на них +-+, выбрали средний
Возвращаемся к замене
Такой переход имели право сделать, так как функция - монотонно возрастающая функция.
2. - парабола с ветвями, направленными вниз, - просто прямая и фигура, образованная при их пересечении будет такова, что кусок параболы будет лежать выше.
Вспомним, что для на некотором интервале, то площадь фигуры будет равна
В нашем случае нужно вычислить пределы, а это как раз абсциссы точек пересечения, то есть нужно решить уравнение
Область допустимых значений (ОДЗ): x >= -4. x - 4*V(x + 4) - 1 < 0 ( V - корень квадратный). x - 1 < 4*V(x + 4) Правая часть неравенства <= 0 для всех х из ОДЗ, левая часть < 0 при x < 1, то есть неравенство выполняется при x < 1, с учетом ОДЗ получаем -4 <= х < 1. Пусть x >= 1. Возведем обе части неравенства в квадрат (x - 1)^2 < 16*(x + 4) x^2 - 2*x + 1 < 16*x + 64 x^2 - 18*x - 63 < 0 Равенство верно на интервале между корнями уравнения. Корни х1 = -3, х2 = 21, неравенство выполняется для -3 < х < 21, с учетом x >= 1 получаем 1 <= х < 21. Объединяем условия -4 <= х < 1 и 1 <= х < 21, получаем ответ: -4 <= х < 21.
1. Пусть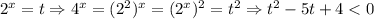
Решать надо методом интервалов, для этого надо найти нули функции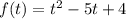
, решим для уравнение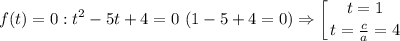 
Получаем разложение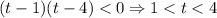
Там интервалы были, знаки на них +-+, выбрали средний
Возвращаемся к замене
Такой переход имели право сделать, так как функция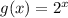
- монотонно возрастающая функция.
2.
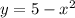- парабола с ветвями, направленными вниз, 
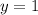- просто прямая и фигура, образованная при их пересечении будет такова, что кусок параболы будет лежать выше.
Вспомним, что для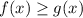
на некотором интервале, то площадь фигуры будет равна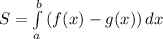 
В нашем случае нужно вычислить пределы, а это как раз абсциссы точек пересечения, то есть нужно решить уравнение