1. Укажите линейное уравнение с двумя переменными.
1) 3·x-5=0 - только одна переменная х
2) х/7-у/5=8/3 - линейное, переменные х и у
3) 7/х+5/у=3/8 - нелинейное
4) 7·x²+5·у=3 - уравнение 2-степени
2. Укажите уравнение, решением которого является пара чисел (1 3/7; 2 5/6) .
Проверим подставкой в уравнение:
1) 14·x-12·y+14=0
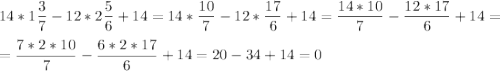
является решением, поэтому остальные уравнение не нужно проверить
2) 14·x-6·y-10=0
3) 10·x/7+17·y/6=27
4) x-6·y=17
3. Какая пара чисел является решением уравнения 3·x-2·y+5=0
1) (-1/3; -2) 2) (-2; -1/3) 3) (-4/3; -1/2) 4) (-3; 2)
Проверим подставкой в уравнение:

не является решением
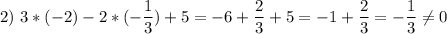
не является решением
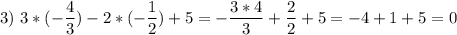
является решением, поэтому последнюю пару не нужно проверить
4. Какая из пар чисел является решением уравнением 2·x-y=6
1) (2; -1) 2) (5; 3) 3) (1; -4) 4) (-1; -3)
Проверим подставкой в уравнение:
1) 2·2-(-1)=4+1=5≠6 - не является решением
2) 2·5-3=10-3=7≠6 - не является решением
3) 2·1-(-4)=2+4=6=6 - является решением, поэтому последнюю пару не нужно проверить
ответ:Второй велосипедист:
Расстояние - 88 км
Скорость - х км/ч
Время в пути - 88/х ч.
Первый велосипедист:
Расстояние - 88 км
Скорость - (х+3) км/ч
Время в пути - 88/ (х+3) ч.
Зная, что второй велосипедист затратил на весь путь больше времени на 3 часа.⇒ Уравнение.
88/х - 88/(х+3)= 3
Избавимся от знаменателя.
88(х+3) - 88х = 3* х*(х+3)
88х +264 - 88х = 3х²+9х
3х²+9х-264 =0
Раздели обе части уравнения на 3:
х²+3х -88=0
D= 9-4*(-88) = 9+352=361
x₁ = (-3-√361) /2 = (-3-19)/2= -11 - не удовл. условию задачи, т.к. скорость не может быть отрицательным значением.
х₂= (-3+19)/2= 16/2=8 км/ч - скорость второго велосипедиста, который и пришел вторым к финишу.
8+3= 11 км/ч - скорость первого велосипедиста
Проверим:
88/8 - 88/11 = 11 ч. - 8 ч.= 3 ч. - разница во времени
ответ: 8 км/ч скорость велосипедиста, который пришел вторым к финишу.
Объяснение: