В решении.
Объяснение:
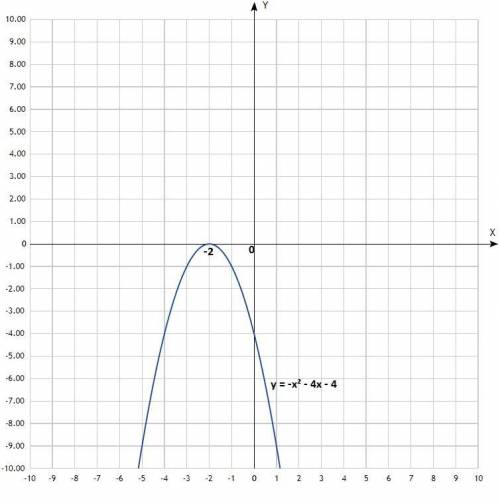
Постройте график функции у = -х2 – 4х – 4. Найти промежутки возрастания и убывания функции.
Дана функция у = -х² - 4х - 4;
Построить график.
График - парабола со смещённым центром, ветви направлены вниз.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = -х² - 4х - 4;
Таблица:
х -5 -4 -3 -2 -1 0 1
у -9 -4 -1 0 -1 -4 -9
По вычисленным точкам построить параболу.
Функция возрастает на промежутке х∈(-∞; -2).
Функция убывает на промежутке х∈(-2; +∞).
угол К=углу Т=48°
Угол В=84°
Объяснение:
Так как ∆ KBT равнобедренный, то угол К=углуТ.
ТМ биссектриса, и значит угол Т поделила на пополам, тогда угол КТМ= углу ВТМ=половине угла К.
Угол ВМТ и угол ВМТ смешные и в сумме дают 180°. , значит угол КМТ=180-72=108°.
Рассмотрим ∆КМТ, так как угол КТМ=1/2 угла КМТ, то возьмем его за х. По сумме угол в треугольнике получаем, х+2х+108°=180°, 3х=72, х=24° это угол КТМ, тогда угол МКТ=2*24=48°=углу К так как-то ∆ КВТ равнобедренный. Значит
угол К=углу Т=48°.
По сумме углов треугольника найдем угол В=180-(48+48) =180-96=84°.
ответ: угол К=углу Т=48°
Угол В=84°
( 8 * ( 12 + 18 ) ) : ( 3 - 2 )
Объяснение:
Можно увеличить значение выражения, если умножить 8 на наибольшее число. Но также благодаря делению мы можем уменьшить значение, поэтому сразу делить - плохая идея. Стоит заметить, что в конце стоит -2, и поэтому мы сможем разделить на наименьшее из возможных чисел (ну, кроме нуля, конечно), т.е на (3-2) = 1.
Итого получаем: (8*12+18):(3-2)
Выгодней будет поставить скобки так (8*(12+18)):(3-2), потому что 18 > 12, и увеличивая число, на которое мы умножаем, мы максимально увеличили произведение.
Мы максимально уменьшили делитель и максимально увеличили делимое, следовательно - (8*(12+18)):(3-2) - наибольший из возможных вариантов.
решение на фото
Объяснение: