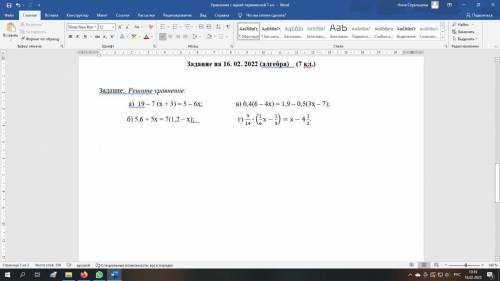
Объяснение: 

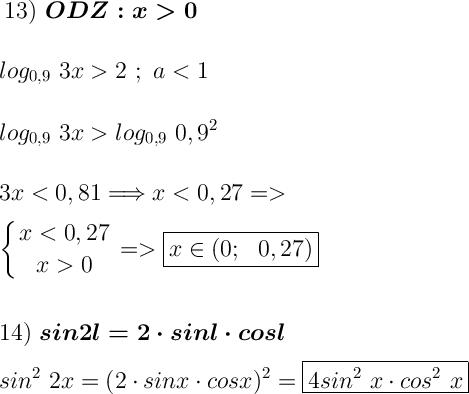

Відповідь:
а) ні
б) так
в) так
г) ні
Пояснення:
Очевидно, що після додавання до парного числа або віднімання від нього одиниці, отримаємо НЕпарне, і навпаки. Уявімо, що гарбузи вже розкладено. Тоді числа гарбузів у будь-яких двох сусідніх кошиках матимуть різну парність.
Нехай у колі розставлено НЕпарну кількість кошиків. Пронумеруємо їх, скажімо, за годинниковою стрілкою. Почнемо для зручності з довільного кошика із НЕпарною кількістю гарбузів. Побачимо, що таке саме непарне число гарбузів міститиме 3-ій кошик (бо в другому — парна кількість гарбузів), 5-ий, ..., останній. Виходить, що в наступному кошику, який під номером "1", повинно бути парне число гарбузів. Але насправді воно НЕпарне. Отримали суперечність.
А от якби було розставлено парну кількість кошиків, то непарне число гарбузів, пронумерованих, як у попередньому абзаці, містив би ПЕРЕДостанній кошик. Тоді останній — парну, а наступний за ним, кошик під номером "1" — знов непарну, як ми й домовлялися.
Отже, здійснити те, що описано в умові задачі, можна, лише якщо використати парну кількість кошиків.
а) х=-45
б) х=7/30
в) х=-30
г) х=4,8
Объяснение:
a) 19-7(x+3) = 5-6x переносим -6х в левую часть, а 19 в правую с противоположными знаками
6х-7(х+3)=5+19 раскрываем скобки, попутно решая вторую часть
6х-7х-21=24 переносим в правую часть "-21" , выполняем действия с иксами
-х=45 меняем знак
х=-45
б) 5,6+5x = 7(1,2-x) раскрываем скобки
5,6+5х = 8,4-7х иксы в левую часть, числа в правую
5х+7х=8,4-5,6 вычисляем
12х=2,8
х=7/30
в) 0,4(6-4x) = 1,9-0,5(3x-7) раскрываем скобки
2,4-1,6х=1,9-1,5х+3,5 иксы в левую часть, числа в правую
-0,1х=3 вычисляем
х=-30