Составить и решить по 5 примеров на применение формулы куб суммы и куб разности

Question

Алгебра: Составить и решить по 5 примеров на применение формулы куб суммы и куб разности

LiudaSerga2345 · Accepted Answer

Пусть скорость первого велосипедиста равна х км/ч, а второго - у км/ч. Первый и второй велосипедисты проехали 25 км их расстояние (x+у)*1=(x+y) км

На расстоянии 30 км первый велосипедист проезжает на 1 ч быстрее другого,т.е. время затраченное первым велосипедистом равно 30/х, а вторым - 30/у. На весь путь затратили (30/x - 30/y) ч.

Решим систему уравнений

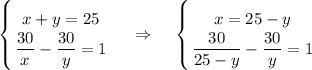
$\displaystyle \left \{ {{x+y=25} \atop {\dfrac{30}{x}-\dfrac{30}{y}=1}} \right. ~~~\Rightarrow~~~\left \{ {{x=25-y} \atop {\dfrac{30}{25-y}-\dfrac{30}{y}=1}} \right.$

Домножим левую и правую части уравнения на (25-y)y ≠ 0 , получим

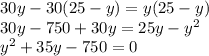
$30y-30(25-y)=y(25-y)\\ 30y-750+30y=25y-y^2\\y^2+35y-750=0$

По теореме Виета

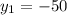y_1=-50 не удовлетворяет условию, так как скорость не может быть отрицательной.

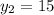y_2=15 км/ч - скорость второго велосипедиста

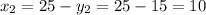x_2=25-y_2=25-15=10 км/ч - скорость первого велосипедиста.

ответ: скорость первого велосипедиста равна 10 км/ч, а второго - 15 км/ч.

MOGZ ответил