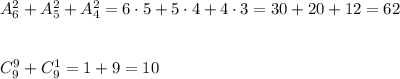
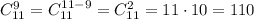
Объяснение: 1) ∫₄⁹√xdx =(2/3)·x√x |₄⁹= (2/3)· (9√9 = 4√4)=(2/3)·(27-8)= 2·19/3=38/3
2) 1+ log₂(x+5) = log₂(3x-1) +log₂(x-1) , ОДЗ: х-1>0, x>1 ⇔ log₂2 +log₂(x+5) = log₂(3x-1) +log₂(x-1) ⇔ log₂ (2x+10) = log₂ (3x²-4x+1) ⇒ 2x+10= 3x²-4x+1 ⇒ 3x²-6x-9 =0⇒ x²-2x - 3=0, D= 4+12=16>0, ⇒x₁=(2+4)/2=3, x₂=(2-4)/2=-1 (не удовлетворяет ОДЗ уравнения). ответ: х=3 №3 tgα=y'(x₀), y'(x)=(x³)'=3x² ⇒ т.к. х₀ =0, то tgα=y'(x₀)=3·0²=0
Объяснение:
1) Нехай: х капкейків спекли за перший тиждень; 3х капкейків спекли другого тижня.
х+3х=356
4х=356
х=89
Відповідь: за перший тиждень кондитери спекли 89 капкейків.
2) Нехай: х метрів - довжина третьої частини; 4х метрів - довжина першої частини; (х+108) метрів - довжина другої частини.
4х+х+х+108=462
6х + 108 = 462
6х = 462 - 108
6х = 354
х = 354 : 6
х = 59
І частина - 4 • 59 м = 236 м
ІІ частина - 59 м + 108 м = 167 м
ІІІ частина - 59 м
3)
a) 3b - (14 - 2b) = -10
3b - 14 + 2b = -10
5b - 14 = -10
5b = -10 + 14
5b = 4
b = 4 : 5
b = 0,8
б) 18 - 4x - 7(2 - x) = 6
18 - 4x - 14 + 7x = 6
-4x + 7x + 18 - 14 = 6
3x + 4 = 6
3x = 2
x = 2/3