417. Найдите числовое значение выражения: 1) 5m' - 10mn +5, при т = 142, n = 42; 5n 2) бm? +12mn + 6n”, при m = 56, n = 44; 3 - . 4 - 3) -36a' + 4a*b - ab', при а = 4, b = 48; 4) — 64а – 8a*b - - ab', при а = -6, b = 84
Дробь — это выражение вида рq , где р и q — многочлены; р — числитель, а q — знаменатель дроби. например: a−bb 2−1 где p = a−b , а q = b 2−1 ; x 2+3y 3+x где p = x 2+3 , а q = y 3+x ; y 2−1y−1 где p = y 2−1 , а q = y−1 . многочлен — это частный случай дроби. например, многочлен y 3+2y+7 равен дроби y 3+2y+71 , а дробь 3x 2+5x−15 можно записать в виде многочлена 35x 2+x− 15 . из курса мы знаем, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. например: 35 = 3•25•2 = 610 . дроби можно преобразовывать аналогичным способом: числитель и знаменатель дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной дроби; числитель и знаменатель дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной дроби, его называют сокращением дроби. данные правила называют основным свойством дроби. рассмотрим примеры. дробь x 2−xx 2 можно заменить на x−1x (числитель и знаменатель разделили на x ). дробь x 2+3xy+1 можно заменить на x 3+3x 2xy+x (числитель и знаменатель умножили на x ). дробь y 2−6y+9y 2−9 можно заменить на (y−3) 2(y−3)(y+3) = y−3y+3 (числитель и знаменатель разделили на y−3 ). равенство y 2−6y+9y 2−9 = y−3y+3 называется тождеством, а преобразование дроби y 2−6y+9y 2−9 в дробь y−3y+3— тождественным преобразованием заданной дроби, в данном случае, сокращением дроби. следует помнить, что тождеством наше равенство является при условии, что y ≠ 3 и y ≠ – 3 , так как знаменатель изначальной дроби при данных значениях переменной обращается в нуль и выражение y 2−6y+9y 2−9 теряет смысл.
Объяснение:
а)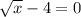 а)
а) 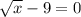
х=16 х=81
б) 1/3х²=3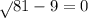
х²=9 х=81
х1=-3 б) 1/2х²=2
х2=3 х²=4
в) -4х²=1/4 х1=-2 х2=2
4х²=-1/4 в) -5х²=1/5
Рівняння не має розв*язків 5х²=-1/5 рівняння розвязків не має
г) -2х²+2,42=0 г) -3х²+2,43=0
-2х²=121/50=0 -3х²+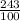 = 0
= 0
-100х²+121=0 -300х²+243=0
-100х²=-121 -300х²=-243
х²=121/100 х²=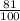
х1=-1,1 х1=-0,9, х2=0,9
х2=1,1