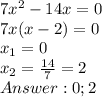
2sin2x + 3sinxcosx - 3cos2x = 1;
Представим 1 в виде суммы по основному тригонометрическому тождеству:
sin2x + 3cosxsinx - 3cos2x = sin2x + cos2x;
Приведем подобные:
sin2x + 3cosxsinx - 4cos2x = 0;
Разделим каждый член уравнения на cos2x:
tg2x + 3tgx - 4 = 0;
Произведем замену и решим квадратное уравнение:
t2 + 3t - 4 = 0;
D = 9 + 16 = 25;
t = (-3 +- 5)/2;
t1 = -4, t2 = 1;
Сделаем обратную замену:
tgx = 1; x = pi/4 + pin, n из Z;
tgx = -4; x = arctg(-4) pin, n из Z.
ответ: pi/4 + pin, n из Z; arctg(-4) pin, n из Z.
Объяснение:
Оцени!
- 1,6.
Объяснение:
Найдем значение выражения - x + 3 * y - z при x = 0,5, y = - 0,9, z = - 1,6.
Для того, чтобы найти значение выражения - x + 3 * y - z, нужно известные значения подставить в само выражение и вычислить его значение. То есть получаем:
- x + 3 * y - z = - 0,5 + 3 * (- 0,9) - (- 1,6) = - 0,5 - 3 * 0,9 + 1,6;
Сначала в порядке очереди вычисляем умножение или деление, потом проводятся действия сложения или вычитания. То есть получаем:
- 0,5 - 3 * 0,9 + 1,6 = - 0,5 - 2,7 + 1,6 = - 3,2 + 1,6 = 1,6.