
Рисунок к задаче в прикрепленном файле.
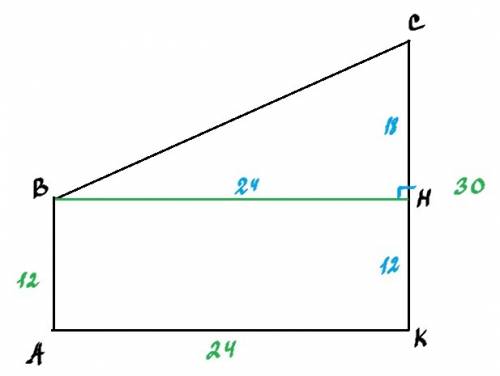
Обозначим длины сосен отрезками: АВ = 12 м, СК = 30 м.
Расстояние между соснами обозначим отрезком АК = 24 м.
Проведем отрезок ВС. Длина этого отрезка равна расстоянию между верхушками сосен.
Геометрическая фигура, которая у нас получилась, прямоугольная трапеция (т.к. мы считаем в идеале, что сосны растут точно перпендикулярно земле, и поверхность земли горизонтальная).
АВСК прмоугольная трапеция с основаниями АВ и СК.
Проведем высоту ВН (см. рисунок).
АВНК - прямоугольник. АК=ВН=24, АВ=НК=12.
СН=СК-КН=30-12=18
Рассмотрим ΔВСН. Он прямоугольный, т.к. ВН⊥СК.
По теореме Пифагора
ВС² = ВН²+СН²
ВС² = 24²+18²=576+324=900
ВС = 30 (м)
ответ: расстояние между верхушками сосен 30 м.
Во-вторых, если функция нечетная, то она симметрична относительно точки О. Поэтому на отрезке -4 <= x <= 0 будет f(x) = |x/2 - 1| - 1
Получаем
2*f(x)*f(x) - 15*f(x) + 7 = 0
По сути получилось квадратное уравнение.
D = 15^2 - 4*2*7 = 225 - 56 = 169 = 13^2
1) f(x) = 1 - |x/2 - 1| = (15 - 13)/4 = 2/4 = 1/2
|x/2 - 1| = 1/2
x/2 - 1 = -1/2; x/2 = 1/2; x1 = 1
x/2 - 1 = 1/2; x/2 = 3/2; x2 = 3
2) f(x) = 1 - |x/2 - 1| = (15 + 13)/4 = 28/4 = 7
|x/2 - 1| = 1 - 7 = -6
Решений нет, значит, формула должна быть другой:
f(x) = |x/2 - 1| - 1 = 7
|x/2 - 1| = 8
x/2 - 1 = 8; x/2 = 9; x3 = 18
x/2 - 1 = -8; x/2 = -7; x4 = -14