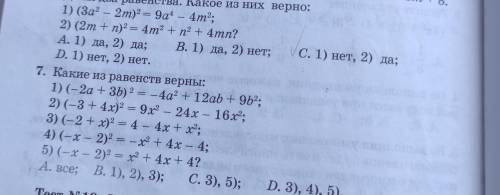
Если нельзя посадить еще одного человека за стол так, чтобы рядом с ним никто не сидел, то максимальное число подряд идущих пустующих стульев равно 2. Т. е. имеем такую последовательность: 2 пустых стула, один занятый, 2 пустых, 1 занятый и т. д. Видим, что данную последовательность можно разбить на тройки (по одному занятому стулу и двум пустым). Поскольку стульев всего 20, а 20 = 3*6 + 2 дает в остатке 2, то у нас выходит 6 занятых стульев плюс еще один занятый, итого минимум 7 человек могут изначально сидеть на стульях.
ответ: 7 человек.
№6²
1) неверно;
2) верно;
С. 1)нет; 2) да.
№7
1) неверно;
2) неверно;
3) верно;
4) неверно;
5) верно;
С.3); 5).
Объяснение:
№6
1) (3а²-2m)²= 9(а²)²-12а²m+4m²;
2) верно;
№7
1) (-2а+3в)²=(3в-2а)²=9в²-12ав+4а²;
2) (-3+4х)²=(4х-3)²=16х²-24х+9;
3) верно;
4) (-х-2)²=-(х+2)²=-(х²+4х+4)=-х²-4х-4;
5) верно;