Из первого произведения:
(πx - 2)(x + Δ) = πx² - 2x + Δπx - 2Δ
Так как квадрат переменной х в правой части равенства имеет коэффициент 2, то π = 2:
2х² - 2х + Δ·2х - 2Δ - 2∀ + 2х = 2х² - 2х + 4
Так как в обеих частях есть 2х² - 2х, то в результате получим:
Δ·2х - 2Δ - 2∀ + 2х = 4
В правой части переменная отсутствует. Следовательно:
Δ·2х = -2х => Δ = -1
Осталось выяснить значение ∀:
-2·(-1) - 2∀ = 4
-2∀ = 2 => ∀ = -1
Окончательно исходное выражение выглядит так:
(2х - 2)(х - 1) - 2(-1 - х) = 2х² - 2х + 4
Проверим:
2х² - 2х - 2х + 2 + 2 + 2х = 2х² - 2х + 4
2х² - 2х + 4 = 2х² - 2х + 4
ответ: Δ = -1; ∀ = -1; π = 2.
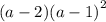
Алгоритм:
Как разложить уравнение высшей степени. По теореме Безу найти корень уравнения. Если найти корень не получается попробовать 1/2 и -1/2. Иначе подбирать (рекомендую ±1/3, ±2/3 и т.п.)
По схеме Горнера или уголком поделить уравнение на (x-a), где a - найденный в пункте 1 корень.
Продолжать до тех пор, пока в качестве одного из множителей не получится квадратное уравнение.
Применить алгоритм разложения на множители квадратного уравнения.
(как делать это быстро: подобрать корень, и подогнать под (x-a))
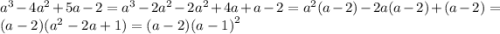
если не правильно простии)