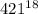- у любого числа, оканчивающегося на 1 в любой целой положительной степени, последняя цифра 1. Тогда число 
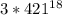оканчивается на цифру 3.
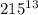- любое число, у которого последняя цифра 5, возведённое в любую целую положительную степень, имеет последнюю цифру 5. Значит, число 
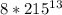оканчивается на цифру 0.
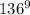- аналогично, любое число, у которого последняя цифра 6, возведённое в в любую целую степень, имеет последнюю цифру 6.
1)упрастила выражение
(у-4)(у+3)+(у+1)^2-(7-у)(у+7) = у^2-у-12+у^2+2у+1+у^2-49 = 3у^2+у-60
2)разложила на множетели
А)21а^2b+28ab^2 = 7ab(3a)+28ab^2 = 7ab(3a)+7ab(4b) = 7ab(3a+4b)
Б)36m^2-100n = 4(9m^2)-100n = 4(9m^2)+4(-25n) = 4(9m^2-25n)
B)125+a^3b^3 = 5^3+a^3b^3 = 5^3+(ab)^3 =
Это формула по которой буду дальше решать её не нужно писать а^3+b^3=(a+b)(a^2-ab+b^2) где а=5 и b=ab
Продолжаем решение
(5+аb)(5^2-5(ab)+(ab)^2) = (5+ab)(25-5ab+a^2b^2)
Г)5x^3-5xy^2 = 5x(x^2-1y^2 = 5x(x+y)(-y)
Объяснение:
^2 это в квадрате
^3 это в кубе
Відповідь:
Пояснення:
Максимальное значение можно определить f'(x)=0
Так как f(0)=f(4)=0, то максимум находится в середине отрезка [0; 4]
|f"(x)|<=4 ‐> |f'(x)|=<4x+C
Так как f(x) имеет корни 0 и 4, то f(x)=ax(x-4)=ax²-4ax
f'(x)=2ax-4a=0 -> x=2
f"(x)=2a -> |a|=<2,
a=2: f(x)=<2x²-8x; f(2)=<8-16=-8
a=-2: f(x)=<-2x²+8x; f(2)=-8+16=8
возможное максимальное значение при х=2 имеем 8