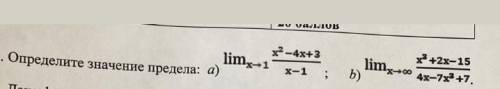
Правило: Если произведение равно нулю, то один из множителей (или все) равен нулю.
Поэтому, мы должны приравнять каждую скобку к нулю и найти корни.
(2x-1)(6x+3)(7x+1)=0
2x-1= 0
2x=1
x=1/2
6x+3 = 0
6x=-3
x=-3/6=-1/2
7x+1 = 0
7x=-1
x=-1/7
ответ: 1/2, -1/2, -1/7
(5-2x)(3x-1)(6+5x)=0
5-2x = 0
-2x=-5
x=5/2
3x-1 = 0
3x=1
x=1/3
6+5x = 0
5x=-6
x=-6/5
ответ: 5/2, 1/3, -6/5
(4x-3)(2x+7)(7x+2)=0
4x-3 = 0
4x=3
x=3/4
2x+7 = 0
2x= -7
x= -7/2
7x+2 = 0
7x= -2
x= -2/7
ответ: 3/4, -7/2, -2/7
3x(2+5x)+x²(5x+2)=0
Раскроем скобки
6x+15x²+5x³+2x²=0
5x³+17x²+6x=0
Вынесем х за скобки
x(5x²+17x+6)=0
Далее действуем по тому же принципу:
x=0
Остальные корни находим через дискриминант:
5x²+17x+6=0
D= 169, √D= 13
x = -2/5
x= -3
ответ: 0, -2/5, -3
x²(4x-1)+5x(4x-1)=0
Можно попробовать другой Он будет быстрее и проще.
(4x-1) - общий множитель, который есть у каждого из слагаемых. Я выделила его жирным шрифтом.
Для удобства мы можем его вынести как обычное чисто.
(4x-1)(x²+5x)=0
(x²+5x) - в это скобке поместилось все то, что осталось после вынесения (4x-1)
Решаем:
(4x-1)(x²+5x)=0
4x-1=0
4x=1
x=1/4
x²+5x=0
x(x+5)=0
x=0
x+5=0
x= -5
ответ: 1/4, 0, -5
(1/5x+2)(2x-1/4)x=0
Тут тоже приравниваем каждый множитель к нулю:
x=0
1/5x+2 = 0
1/5x = -2
x = -10
2x-1/4 = 0
2x=1/4
x=1/8
ответ: 0, -10, 1/8
(-3; 2; -5); (3; -2; 5)
Объяснение:
(x+y)(x+z)=8
(x+y)(y+z)=3
(y+z)(x+z)=24
(x+y)(x+z)(x+y)(y+z)(y+z)(x+z)=8·3·24
(x+y)²(x+z)²(y+z)²=24·24
[(x+y)(x+z)(y+z)]²=24²
(x+y)(x+z)(y+z)=±24
1) (x+y)(x+z)(y+z)=-24
-24=(x+y)(x+z)(y+z)=8(y+z)⇒y+z=-3
-24=(x+y)(x+z)(y+z)=3(x+z)⇒x+z=-8
-24=(x+y)(x+z)(y+z)=24(x+y)⇒x+y=-1
y+z=-3
x+z=-8
x+y=-1
(y+z)+(x+z)+(x+y)=-3+(-8)+(-1)
2(x+y+z)=-12
x+y+z=-6
x=(x+y+z)-(y+z)=-6-(-3)=-3
y=(x+y+z)-(x+z)=-6-(-8)=2
z=(x+y+z)-(x+y)=-6-(-1)=-5
2) (x+y)(x+z)(y+z)=24
24=(x+y)(x+z)(y+z)=8(y+z)⇒y+z=3
24=(x+y)(x+z)(y+z)=3(x+z)⇒x+z=8
24=(x+y)(x+z)(y+z)=24(x+y)⇒x+y=1
y+z=3
x+z=8
x+y=1
(y+z)+(x+z)+(x+y)=3+8+1
2(x+y+z)=12
x+y+z=6
x=(x+y+z)-(y+z)=6-3=3
y=(x+y+z)-(x+z)=6-8=-2
z=(x+y+z)-(x+y)=6-1=5
1) Раскладываем числитель на множители и сокращаем дробь.
2) Делим многочлены, стоящие в числителе и в знаменателе на старшую степень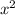 .
.