(см. объяснение)
Объяснение:
Данная задача имеет более одного решения.
Первый :
В прямоугольном треугольнике гипотенуза будет равна двум медианам, поэтому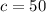 
. Площадь треугольника найдем по формуле 
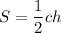, откуда 
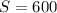. С другой стороны 
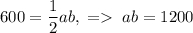. По теореме Пифагора 
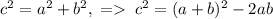. Подставляем c и ab в формулу: 
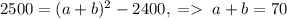. Тогда искомый периметр равен 
.
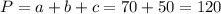Второй :
Возможно было записать две теоремы Пифагора и найти катеты, как:
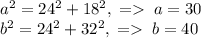
Тогда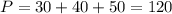 
.
Здесь предварительно была использована теорема Пифагора для образованного высотой и медианой треугольника:
.
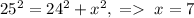Тогда вс длины равны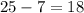 
и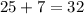 
.
Задача решена!
Пусть масса равна 60 кг.
число полных квадратиков - 592.
Число неполных - 80.
Найдем площадь подошвы:
(592+(80/2))*(1/4)= 158 см²
Переведем в систему СИ:
S1= 158 см² = 0,0158 м².
Выражение, для определения давления тела на плоскость имеет вид:
P=F/S , где F - сила давления на плоскость, S - площадь плоскости.
В нашем случае сила давления, это вес:
F=m*g
Площадь одной ноги:
S1=0,0158 м²
Площадь опоры, когда стоишь:
S=2*S1
После поставления этих выражений в формулу давления, получаем:
Когда идешь, площадь опоры одна нога:
P=m*g/(S1)=60*9,8/0,0158= 37215,1 Па.
Когда стоишь, площадь опоры две ноги:
P=m*g/(S)=60*9,8/(2*0,0158)= 18607,5 Па.
ответ: давление стоя на месте 18,6075 кПА, при ходьбе 37,2151 кПа, получается, при ходьбе давление больше, т.к весь вес приходится на одну ногу, а площадь опоры вдвое меньше.
ответ: при х=0 у=1
при у=0 х=3п/2+2пn, n - целые числа