Не выполняя построения, найди координаты точек пересечения графика уравнения с осеями координат

👇

Увидеть ответ

Ответ:

zaijiki

27.05.2022

1. с Ox: -4x+6=0, x=1,5

c Oy: 6=3y, y=2

2. c Ox: x^2=9, x=-3;3

c Oy: y=9

4,5(81 оценок)

Ответ:

Qkoddk

27.05.2022

В решении.

Объяснение:

Не выполняя построения, найди координаты точек пересечения графика уравнения с осями координат;

1) -4х + 6 = 3у

Преобразовать уравнение в уравнение функции:

3у = -4х + 6

↓

3у = 6 - 4х

↓

у = (6 - 4х)/3

у = 2 - 4х/3;

а) Любой график пересекает ось Оу при х равном нулю:

х = 0;

у = 2 - 0/3

у = 2;

Координаты точки пересечения прямой с осью Оу: (0; 2);

б) Любой график пересекает ось Ох при у равном нулю:

2 - 4х/3 = 0

-4х/3 = -2

-4х = -6

х = -6/-4 (деление)

х = 1,5;

Координаты точки пересечения прямой с осью Ох: (1,5; 0);

2) у + х² = 9;

Преобразовать уравнение в уравнение функции:

у = 9 - х²;

а) Любой график пересекает ось Оу при х равном нулю:

х = 0;

у = 9 - 0

у = 9;

Координаты точки пересечения прямой с осью Оу: (0; 9);

б) Любой график пересекает ось Ох при у равном нулю:

9 - х² = 0

-х² = -9/-1

х² = 9

х = ±√9

х = ±3;

Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х= -3 и х = 3.

Координаты точек пересечения параболы с осью Ох: (-3; 0); (3; 0).

ответы:

1. с Ох (1,5; 0), с Оу (0; 2);

2. с Ох (-3; 0); (3; 0); с Оу (0; 9).

4,4(91 оценок)

Открыть все ответы

Ответ:

August333

27.05.2022

Уравнение НОК (х², y) + НОК (х, у²) = 1996 не имеет решения в натуральных числах.

Объяснение:

x, y - взаимно простые числа (НОД (x,y)=1, x≠y)

x,y∈ N

НОК (x², y)=x²y

НОК (x, y²)=xy²

НОК (x², y) + НОК (x, y²) = 1996

x²y+xy²=1996

xy(x+y)=2²·499

xy(x+y)=1·4·499⇒ x=1, y=4, x+y ≠ 499

или

xy(x+y)=1·499·4⇒ x=1, y=499, x+y≠4

или

xy(x+y)=4·1·499⇒ x=4, y=1, x+y ≠499

или

xy(x+y)=4·499· 1⇒ x=4, y=499, x+y ≠1

или

xy(x+y)=499·1·4⇒ x=499, y=1, x+y ≠4

или

xy(x+y)=499·4·1⇒ x=499, y=4, x+y ≠1

Уравнение не имеет решения в натуральных числах.

x, y – не взаимно простые числа

x,y∈ N

НОД (x,y)=k

x=km

y=kn

k,m,n∈N

НОК (x², y)= НОК (k²m², kn )=k²m²n

НОК (х, у²)= НОК (km, k²n²)= k²mn²

НОК (x², y) + НОК (x, y²) = 1996

k²m²n+ k²mn²=1996

k² mn(m + n)= 2²·499

k²=2² ⇒ k=2

mn(m + n)=499

499 - простое число

Уравнение не имеет решения в натуральных числах.

4,5(81 оценок)

Ответ:

hren4

27.05.2022

1/2

Объяснение:

Попробуем разложить знаменатель на множители:

25n^2 - 5n - 6 = 0

D = 25 - 4*25*(-6) = 25 + 600 = 625 = 25^2

n1 = (5 - 25)/50 = -20/50 = -2/5

n2 = (5 + 25)/50 = 30/50 = 3/5

25n^2 - 5n - 6 = (5n + 2)(5n - 3)

Предположим, что дробь является суммой дробей:

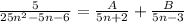
$\frac{5}{25n^2-5n-6}=\frac{A}{5n+2} + \frac{B}{5n-3}$

Вычислим А и В:

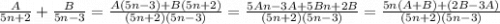
$\frac{A}{5n+2} + \frac{B}{5n-3}=\frac{A(5n-3)+B(5n+2)}{(5n+2)(5n-3)} =\frac{5An-3A+5Bn+2B}{(5n+2)(5n-3)} =\frac{5n(A+B)+(2B-3A)}{(5n+2)(5n-3)}$

Знаменатели равны, значит, числители тоже равны. Система:

{ A + B = 0

{ 2B - 3A = 5

Решаем подстановкой:

{ A = -B

{ 2B + 3B = 5

B = 1, A = -1

Получили такую разность:

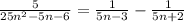
$\frac{5}{25n^2-5n-6}=\frac{1}{5n-3} - \frac{1}{5n+2}$

Подставляем эту разность в нашу формулу ряда:

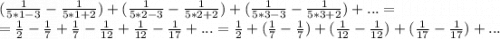
$(\frac{1}{5*1-3} - \frac{1}{5*1+2}) + (\frac{1}{5*2-3} - \frac{1}{5*2+2})+(\frac{1}{5*3-3} - \frac{1}{5*3+2})+...=\\ =\frac{1}{2}-\frac{1}{7}+\frac{1}{7}-\frac{1}{12}+\frac{1}{12} -\frac{1}{17} +...=\frac{1}{2}+(\frac{1}{7}-\frac{1}{7})+(\frac{1}{12}-\frac{1}{12}) +(\frac{1}{17}-\frac{1}{17}) +...$