Дробь 
является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
.
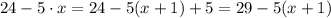Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
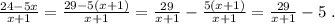
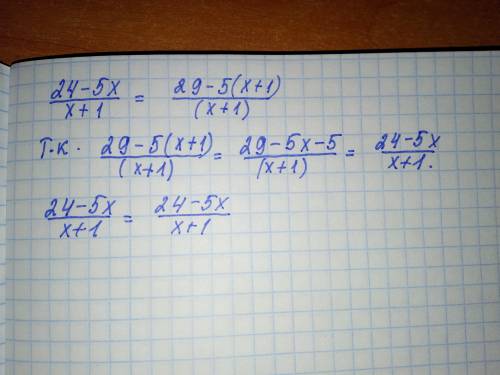
20.000.220
Моя логика:
• число точно восьмизначное, значит, первой цифрой будет 2, чтобы очертить количество знаков
• раз число делится на круглое число (30), значит, оно должно оканчиваться на 0
• осталось только выбрать количество двоек: число, делящееся на 30, должно делиться на 3. Число делится на 3, если сумма всех его цифр делится на 3. Минимальное количество двоек в этом случае будет равно трём: 2+2+2=6, делится на 3 без остатка
• все двойки, кроме первой, расположим как можно ближе к концу, чтобы получить как можно меньшее число
общий знаменатель x(x-4)
14x - 4(x-4) = 3*x(x-4)
14x - 4x + 16 - 3x^2 + 12x = 0
3x^2 - 22x -16 = 0
D = 22*22 - 4*3*16 = 2*11*2*11 - 4*3*16 = 4*(121 - 48) = 4*73
x1 = (22 + 2корень(73)) / 6 = (11+корень(73)) / 3
x2 = (22 - 2корень(73)) / 6 = (11-корень(73)) / 3