Пусть функция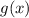 
чётна. По определению это значит, что 
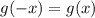. Получим:
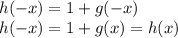
Это значит, что функция 
тоже чётна.
Теперь пусть функция 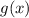нечётна. По определению это значит, что 
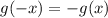. Получим:
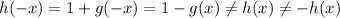
Это значит, что функция не является ни чётной, ни нечётной (за исключением случая, когда функция g(x) является нулевой константой).
ответ: если g(x) чётна, то h(x) тоже чётна. Если g(x) нечётна, то h(x) не является ни чётной, ни нечётной (за исключением случая, когда g(x) является нулевой константой, — тогда h(x) является чётной).
х км/ч - собственная скорость катера;
(х + 2) км/ч - скорость катера по течению реки;
(х - 2) км/ч - скорость катера против течения реки.
16/(х + 2) ч - время прохождения катером 16 км по течению реки;
12/(х - 2) ч - время прохождения катером 12 км против течения реки.
На весь путь катер затратил (16/(х + 2) + 12/(х - 2)) ч или 5 ч.
Получается уравнение 16/(х + 2) + 12/(х - 2) = 5.
О. Д. З. х ≠ ±2;
16(х - 2) + 12(х + 2) = 5(х² - 4);
16х - 32 + 12х + 24 = 5х² - 20;
28х - 8 = 5х² - 20;
5х² - 28х - 20 + 8 = 0;
5х² - 28х - 12 = 0;
D = b² - 4ac;
D = (-28)² - 4 * 5 * (-12) = 1024; √D = 32;
x = (-b ± √D)/(2a);
x1 = (28 + 32)/(2 * 5) = 60/10 = 6 (км/ч);
х² = (28 - 32)/10 = -0,4 - скорость не может быть отрицательной.
ответ. 6 км/ч