В решении.
Объяснение:
d) |4 - x| < 5
Схема:
4 - x < 5; 4 - x > -5
-x < 5 - 4 -x > -5 - 4
-x < 1 -x > -9
x > -1 x < 9
(знак неравенства меняется при умножении или делении на минус).
Решение неравенства: х∈(-1; 9).
Неравенство строгое, скобки круглые.
е) |3x - 9| + 2 > 7
|3x - 9| > 7 - 2
|3x - 9| > 5
Схема:
3x - 9 > 5 3x - 9 < -5
3x > 5 + 9 3x < -5 + 9
3x > 14 3x < 4
x > 14/3 x < 4/3
Решение неравенства: (-∞; 4/3)∪(14/3; +∞).
Неравенство строгое, скобки круглые.
f) |3x + 2| - 1 >= 10
|3x + 2| >= 10 + 1
|3x + 2| >= 11
Схема:
3x + 2 >= 11 3x + 2 <= -11
3x >= 11 - 2 3x <= -11 - 2
3x >= 9 3x <= -13
x >= 3 x <= -13/3
Решение неравенства: (-∞; -13/3]∪[3; +∞).
Неравенство нестрогое, скобки квадратные, а знаки бесконечности всегда с круглой скобкой.
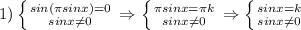
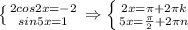
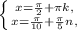
Можно сравнить (1/2)^2=1/4 (1/2)^3=1/8 1/4 - 1/8 = 1/8
(1/3)^2=1/9 (1/3)^3=1/27 1/9 -1/27=2/27 2/27<1/8
11^-5=(1/11)^5 <1
(5/6)^2/3<1
0,15^-3= (25/3)^3 >1
1,2 ^-2=(6/5)^-2=(5/6)^2 <1