а) f(x) = x/5 + 1
x/5 + 1 < 0 ⇒ x/5 < -1 ⇒ x < -5
f(x) < 0 при х ∈ (-∞; -5)
f(x) = 0 при х = -5
f(x) > 0 при х ∈ (-5 ; +∞)
б)
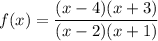
Решаем задачу методом интервалов
1) находим точки нулевых значений функции
х - 4 = 0 ⇒ х = 4
х + 3 = 0 ⇒ х = -3
2) находим точки разрыва функции
х - 2 = 0 ⇒ х = 2
х + 1 = 0 ⇒ х = - 1
Делим числовую прямую на интервалы и определяем знаки функции в этих интервалах
---( + )-------- -3 ---( - )-------- -1 ----( + )---------- 2 ----( - )---------- 4 ------(+) ----------
f(x) < 0 при х ∈ (-3; -1)∪(2; 4)
f(x) > 0 при х ∈ (-∞; -3)∪(-1; 2)∪(4; +∞)
ответ.
Это линейное дифф. ур-е 1 порядка. Решаем с замены.