Если две величины связаны между собой так, что с увеличением (уменьшением) значения одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз, то такие величины называются прямо пропорциональными.
О таких величинах говорят также, что они связаны между собой прямо пропорциональной зависимостью.
В природе и в окружающей нас жизни встречается множество подобных величин. Приведём примеры:
1. Время работы (день, два дня, три дня и т. д. ) и заработок, полученный за это время при подённой оплате труда.
2. Объём какого-нибудь предмета, сделанного из однородного материала, и вес этого предмета.
Прямая пропорциональность имеет вид: у=кх+С, где К-угловой коэффициент, на который умножается Х, а С- свободный член для нашего уравнения у=3х-7 к=3, С= -7, чтобы составить уравнение функции, параллельной данной и проходящей через начало координат, вспомним условие параллельности прямых: к₁=к₂, а чтобы график через начало координат С должно быть =0, тогда если к₂=к₁=3, а С=0. запишем искомое уравнение у=3х+0, у=3х-график этого параллелен графику у=3х-7 и проходит через начало координат точку О(0;0)
Нет точки максимума
Объяснение:
Рассмотрим функцию
Так как в составе функции участвует квадратный корень, то область определений функции: x≥0, то есть D(y)=[0; +∞).
Чтобы найти экстремумы (локальные минимумы и максимумы) будем исследовать функцию с производной функции. Вычислим производную функции:
Так как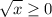 , то
, то
для любого x∈D(y). Это означает, что данная функция монотонно возрастает в D(y). Отсюда следует, что у функции нет точки максимума.
Так как функция монотонно возрастает в D(y), то минимальное значение в D(y)=[0; +∞) принимает при x=0: y(0)=2.