Question

решить систему

при решении иррацтонального неравенства использовать такие равносильные претворения

система +система + объединение систем

Answer 1

$\left\{\begin{array}{l}\sqrt{2x-1} x-2\\x-2 < 0\end{array}\right$    

Решаем первое неравенство системы по правилу:

    $\sqrt{f(x)} g(x)\ \ \Longleftrightarrow \ \ \left[\begin{array}{l}\left\{\begin{array}{l}g(x)\geq 0\\f(x) g^2(x)\\\end{array}\right\\\left\{\begin{array}{l}g(x) < 0\\f(x)\geq 0\end{array}\right\end{array}\right\end{array}\right$

$1)\ \ \sqrt{2x-1} x-2\ \ \Rightarrow \ \ a)\ \left\{\begin{array}{l}x-2\geq 0\\2x-1 (x-2)^2\end{array}\right\ \ ili\ \ b)\ \left\{\begin{array}{l}x-2 < 0\\2x-1\geq 0\end{array}\right$

$a)\ \left\{\begin{array}{l}x-2\geq 0\\2x-1 (x-2)^2\end{array}\right\ \ \left\{\begin{array}{l}x\geq 2\\2x-1 x^2-4x+4\end{array}\right\ \ \left\{\begin{array}{l}x\geq 2\\x^2-6x+5 < 0\end{array}\rightleft\{\begin{array}{l}x\geq 2\\(x-1)(x-5) < 0\end{array}\right\ \ \left\{\begin{array}{l}x\in [\ 2\ ;+\infty )\\x\in (\, 1\, ;\, 5\, )\end{array}\right\ \ \Rightarrow \ \ x\in [\ 2\ ;\ 5\ )$

Квадратное неравенство решали методом интервалов:  

$\star \ x^2-6x+5=0\ \ ,\ \ x_1=1\ ,\ x_2=5\ \ \ (teorema\ Vieta)x^2-6x+5=(x-1)(x-5) < 0\ \ ,znaki:\ \ +++(1)---(5)+++\ \ \ ,\ \ \ x\in (\, 1\, ;\, 5\, )\ \ \star$  

$b)\ \left\{\begin{array}{l}x-2 < 0\\2x-1\geq 0\end{array}\right\ \ \left\{\begin{array}{l}x < 2\\x\geq 0,5\end{array}\right\ \ \ \Rightarrow \ \ \ x\in [\ 0,5\ ;\ 2\ )$  

Теперь объединим решения 1 и 2 систем , получим решение 1) иррационального неравенства заданной системы .

$c)\ \ \left[\begin{array}{l}x\in [\, 2\, ;\, 5\, )\\x\in[\ 0,5\ ;\ 2\ )\end{array}\right\ \ \Rightarrow \ \ \bf x\in [\, 0,5\, ;\, 5\, )$    

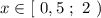Итак, $x\in [\ 0,5\ ;\ 2\ )$ - это решение первого неравенства заданной системы.

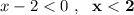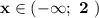2) Решаем второе неравенство заданной системы:   $x-2 < 0\ ,\ \ \bf x < 2$  ,  $\bf x\in (-\infty ;\ 2\ )$  .

3) Теперь найдём решение заданной системы как пересечение решений 1-го и 2-го неравенств заданной системы .

$d)\ \ \left\{\begin{array}{l}x\in [\, 0,5\, ;\, 5\, )\\x\in (-\infty ;\ 2\ )\end{array}\right\ \ \Rightarrow \ \ \bf x\in [\, 0,5\, ;\, 2\, )$  

ответ:  $\bf x\in [\ 0,5\, ;\, 2\, )$   .  

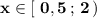 Можно отметить, что все эти процедуры выполнять не обязательно, так как в условии системы уже задано, что  х-2<0 , а (х-2) - это правая часть 1-го неравенства. То есть специально рассматривать случай, когда  х-2≥0 не нужно и пункт а) отпадает . Решаем сразу первое неравенство с пункта b) . Как видно по ответу, решением заданной системы  является решение системы b) .