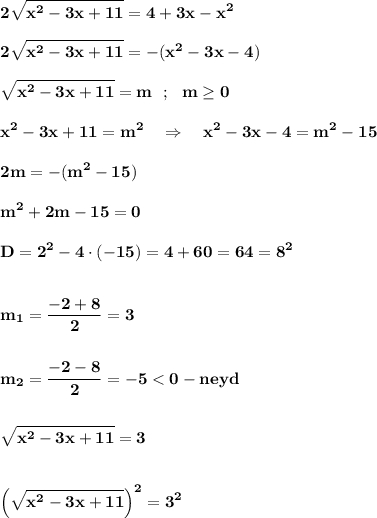

Проверкой убеждаемся , что подходят оба корня .
ответ : 1 ; 2
1.Найти экстремумы функций:
1) f(x)=х^3-х^2-х +2 2) f(x)= (8 -7х)*е^х
2.Найти интервалы возрастания и убывания функции f(x)=х^3-х^2-х +2
1
1)f`(x)=3x²-2x-1=0
D=4+12=16
x1=(2-4)/6=-1/3
x2=(2+4)/6=1
+ _ +
(-1/3)(1)
max min
ymax=-1/27-1/9+1/3+2=(-1-3+9+54)/27=59/27
ymin=1-1-1+2=1
2)f`(x)=-7e^x+(8-7x)e^x=e^x*(-7+8-7x)=0
1-7x=0
x=1/7
+ _
(1/7)
max
ymax=(8-1)*e^(1/7)=e^(1/7)
2
f`(x)=3x²-2x-1=0
D=4+12=16
x1=(2-4)/6=-1/3
x2=(2+4)/6=1
+ _ +
(-1/3)(1)
возр убыв возр
3
смотреть 1
x=-1/3∈[-1;3/2]
x=1∈[-1;3/2]
y(-1)=-1-1+1+2=1
y(-1/3)=59/27 наиб
4
y(1)=1
y(3/2)=27/8-9/4-3/2+2=(27-27-12+16)/8=1/2 наим
5
f`(x)=3x²-2x-1
f``(x)=6x-2 прямая проходит через точки (0:-2) и (1;4)
Объяснение:
Делаем замену x^2 -3x = t => D(f) на t: t+11 >=0 , 4 - t>=0 => -11<=t<=4
уравнение имеет вид 2*sqrt(t+11) = t-4
возводим в квадрат, приводим подобные и получаем уравнение вида t^2-12t-28, далее теорема Виета, получаем, что t1 = 14, t2 = -2 что удовлетворяет указанному выше промежутку. Делаем обратную замену и получаем, что x = 1 , x = 2, что также удовлетворяет нам. Все есть на фото.