Question

Доведіть що при всіх цілих значеннях n виразу (n-2)(n-1)n(n+1) +1 є квадратом цього числа

Answer 1

(n-2)(n-1)n(n+1) +1 = ( n² -n - 1 )²

Объяснение:

доведіть що при всіх цілих значеннях n виразу (n-2)(n-1)n(n+1) +1 є квадратом цього числа

$(n-2)(n-1)n(n+1) + 1$

Сгруппируем множители :

$\Big ((n-2)(n+1) \Big ) \cdot \Big( n (n-1)\Big ) + 1 = = (n^2 -n - 2)(n^2-n)+ 1$

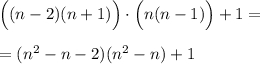
Сделаем замену :

$u = n^ 2 - n$

$\implies ( u -2) \cdot u + 1 = u ^2 -2u +1 = (u-1)^2$

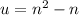
Подставим   u = n² -n

$(u-1)^2 = (n^2 -n-1)^2$

Доказано  , что при любом  целом  n  выражение (n-2)(n-1)n(n+1) +1   является   полным квадратом