Question

сделать.
завтра в 8:30 нужно сдать..

Answer 1

См. рис.

Объяснение:

Каждое из уравнений примера имеет вид $\[y = kx + b,\]$ т. е. задает прямую. Для построения прямой достаточно найти две произвольные точки, принадлежащие ей, и соединить их линией.

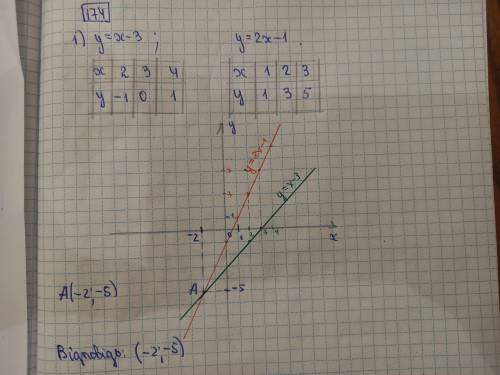
Например, для прямой $\[y = x - 3\]$ можно взять $\[x = 3,\]$ тогда $\[y = 3 - 3 = 0;\]$ и $\[x = 0,\]$ тогда

$\[y = 0 - 3 = - 3\]$ (красная линия на рисунке 1).

Для прямой $\[y = 2x - 1\]$ можно взять $\[x = 0,\]$ тогда $\[y = 2 \cdot 0 - 1 = - 1;\]$ и $\[x = 1,\]$ тогда $\[y = 2 \cdot 1 - 1 = 1\]$ (синяя линия на рисунке 1).

Аналогично для второго примера.

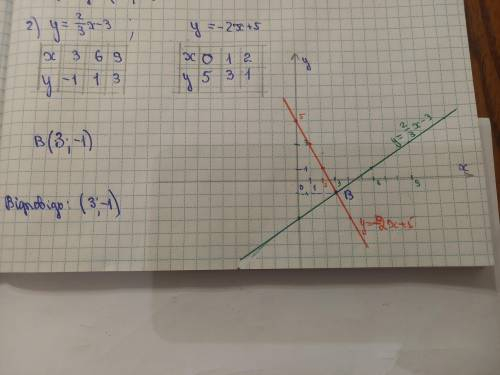
Чтобы получить целые точки, желательно выбрать два значения аргумента, кратные 3. Например, при  $\[x = 3\ y = \displaystyle\frac{2}{3} \cdot 3 - 3 = - 1;\]$ для $\[x = 0\ y = \displaystyle\frac{2}{3} \cdot 0 - 3 = - 3\]$ (красная линия на рисунке 2).

Для второго графика можно взять $\[x = 1,\]$ тогда $\[y = - 2 \cdot 1 + 5 = 3;\]$$\[x = 3,\]$ тогда $\[y = - 2 \cdot 3 + 5 = - 1\]$ (синяя линия на рисунке 2).

Answer 2

Розв'язання завдання додаю.

Спокійної нам всім ночі