Question

дано пряму 2x - y + 4 = 0 і точку А(1;1). через точку А проведено пряму, паралельну даній, і пряму, перпендикулярну до данної. складіть рівняння цих прямих

Answer 1

Параллельная прямая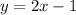 $y = 2x - 1$,  перпендикулярная прямая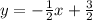 $y = - \frac{1}{2}x + \frac{3}{2}$

Объяснение:

Перепишем уравнение прямой в виде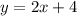 $y = 2x + 4$.

Тогда прямая, параллельная данной, имеет тот же угловой коэффициент, то есть записывается в виде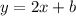 $y = 2x + b$.

Так как эта прямая проходит через точку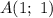 $A(1;\,\,1)$, эти координаты должны удовлетворять этому уравнению:

$1 = 2 \cdot 1 + b;b = - 1.$

Значит искомое уравнение параллельной прямой: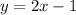 $y = 2x - 1$.

Угловые коэффициенты перпендикулярных прямых в произведении дают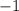 $-1$. Поэтому уравнение прямой, перпендикулярной данной, записывается в виде

$y = - \displaystyle\frac{1}{2}x + b.$

Так как и эта прямая проходит через точку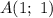 $A(1;\,\,1)$, эти координаты должны удовлетворять этому уравнению:

$1 = - \displaystyle\frac{1}{2} \cdot 1 + b;b = \displaystyle\frac{3}{2}.$

Значит искомое уравнение перпендикулярной прямой:

$y = - \displaystyle\frac{1}{2}x + \displaystyle\frac{3}{2}.$