Объяснение:
Сумма 1+3+...+(2n-1) значит сумму всех нечетных натуральных чисел начиная с 1 и заканчивая 2n-1
Так как при n=1 =>2n-1=2*1-1=1, то для базы индукции сумма начинается с 1 и ею же заканчивается, т.е. состоит только из одного числа 1,
а уже при n=2 (1+3), n=3 (1+3+5) и т.д., и больше будет два и больше слагаемых, и последний член предстанет "более явно",
при n=1 : 1+3+...+(2n-1) =1=(2n-1)
формула 2n-1 показывает какой вид имеет n-ое слагаемое суммы, но в случае n=1 сумма состоит из одного единственного слагаемого 1
Объяснение:
В первой системе очень удобно выразить х, и подставить во второе уравнение. После чего открываем скобки и приводим подобное.
Получаем квадратное уравнение, я умножила всё на -1 чтобы было удобнее.
Можно воспользоваться теоремой Виета, дискриминантом и т.д
Я для раскрытия квадратного многочлена использую такую формулу
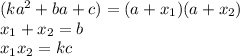
при этом, если k>0 уравнение следует записать в таком виде

и только потом выносить общий множитель за скобку.
В первом уравнении второй системы у нас разность квадрата, после того как мы нашли ее, можем возвести правую и левую части в корень, и извлечь его. После этого выражаем одну переменную через другую и ищем корни уравнения.


Для того чтобы найти значение аргумента, при котором функция y = 4x + 3 принимает значение равное 12, нужно решить уравнение:
4x + 3 = 12
Вычтем 3 из обеих частей уравнения:
4x = 9
Разделим обе части на 4:
x = 9/4
Таким образом, значение аргумента, при котором функция y = 4x + 3 принимает значение равное 12, равно 9/4.