Question

Знайдіть найбільше та найменше значення функції y = (x ^ 2 + 4)/(2x - 3) на проміжку [0;5]

Answer 1

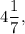наибольшее значение функции равно $4\dfrac{1}{7} ,$  а наименьшее значение функции равно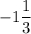   $-1\dfrac{1}{3}$

Объяснение:

Найти наибольшее и наименьшее значение функции

$y=\dfrac{x^{2} +4}{2x-3}$     на промежутке [ 0; 5]

Так как делить на нуль нельзя, то 2х -3 ≠0, то есть х ≠ 1,5.

Тогда область определение функции: D(y) = ( -∞ ; 1,5 ) ∪(1,5; + ∞)

Найдем производную функции

$y'=\left(\dfrac{x^{2} +4}{2x-3}\right)'= \dfrac{(x^{2} +4)'(2x-3) - (x^{2} +4)(2x-3)'}{(2x-3)^{2} } ==\dfrac{2x\cdot(2x-3) -2\cdot( x^{2} +4)}{(2x-3)^{2} } =\dfrac{4x^{2} -6x-2x^{2} -8}{(2x-3)^{2} } =\dfrac{2x^{2} -6x -8}{(2x-3)^{2} }$

Найдем критические точки, решив уравнение: y' = 0.

Дробь равна нулю, если числитель равен нулю

$2x^{2} -6x -8=0|:2;\\x^{2} -3x-4=0;\\D =(-3)^{2} -4\cdot1\cdot (-4)= 9+16=25 =5^{2} ;x{_1}= \dfrac{3-5}{2} =-\dfrac{2}{2} =-1;x{_2}= \dfrac{3+5}{2} =\dfrac{8}{2} =4.$

Заданному промежутку [ 0; 5]  принадлежит х =4.

Найдем значение функции на концах промежутка и в точке х =4 .

$y(0)=\dfrac{0^{2} +4}{2\cdot 0-3}=\dfrac{4}{-3} =-1\dfrac{1}{3} ;y(4)=\dfrac{4^{2} +4}{2\cdot4-3}=\dfrac{16+4}{8-3} =\dfrac{20}{5} =4;y(5)=\dfrac{5^{2} +4}{2\cdot5 -3}=\dfrac{25+4}{10-3} =\dfrac{29}{7} =4\dfrac{1}{7} .$

Сравним найденные значения и получим, что наибольшее значение функции равно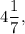 $4\dfrac{1}{7} ,$  а наименьшее значение функции равно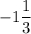   $-1\dfrac{1}{3}$

#SPJ1