<!--c-->
Преобразим заданное уравнение:
x3+12x2−27x=a
С производной построим график функции y=x3+12x2−27x.
1. Введём обозначение f(x)=x3+12x2−27x.
Найдём область определения функции D(f)=(−∞;+∞).
2. Найдем стационарные и критические точки, точки экстремума и промежутки монотонности функции:
f′(x)=(x3+12x2−27x)′=3x2+24x−27.
Внутренние точки области определения функции, в которых производная функции равна нулю, назывём стационарными, а внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, —критическими.
Производная существует всюду в области определения функции, значит, критических точек у функции нет. Стационарные точки найдем из соотношения f′(x)=0:
3x2+24x−27=0|÷3x2+8x−9=0D4=(b2)2−ac=822+9=25x1,2=−b2±D4−−√a=−82±25−−√1=−82±5x1=−82−5=−9x2=−82+5=1
Критические и стационарные точки делят реальную числовую прямую на интервалы с неизменным знаком производной. Чтобы определить знак производной, достаточно вычислить значение производной функции в какой-либо точке соответственного интервала.
Если производная функции в критической (стационарной) точке:
1) меняет знак с отрицательного на положительный, то это точка минимума;
2) меняет знак с положительного на отрицательный, то это точка максимума;
3) не меняет знак, то в этой точке нет экстремума.
Итак, определим точки экстремума:
При x<−9 имеем положительную производную (на этом промежутке функция возрастает); при −9<x<1 имеем отрицательную производную (на этом промежутке функция убывает). Значит, x=−9 — точка максимума функции. При −9<x<1 имеем отрицательную производную, при
Объяснение:
1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.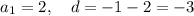 
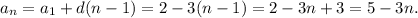
8)
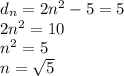
ответ: нет, не является, потому что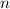 
должно быть натуральным числом.
9) 
Наибольшее натуральное 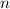, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
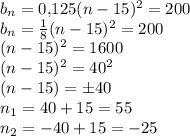
Второе решение не подходит, поскольку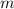 
должно быть натуральным числом.
ответ: 
Відповідь:
Пояснення:
1) (-2;-4)
2) x₁=-4; x₂=0
3) -4 < x <0
4)
зростає x>-2
спадає х <-2
5) -4