

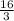
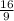
 или х₂ = 1
или х₂ = 1
5
Объяснение:
Можно попробовать метод подбора, но тут все предельно просто. Нам даже не важно сколько шариков, куда важнее их разнообразие. Чтобы два шарика имели одинаковый цвет, нужно чтобы других вариантов не оставалось, то есть чтобы ты взял либо все цвета по отдельности, либо одного цвета. То есть представим ситуацию: берём шарик (белый), второй (красный), третий (зелёный), четвертый (синий), а пятый в любом случае будет либо белым, либо зелёным, либо синим. Также может повезти, но это мы не берём в расчет. Поэтому ответ 5. Если возьмём 4, то с малой вероятностью может произойти представленная мною ситуация (хоть и шанс мал, но он есть)
Для розв'язання рівняння методом заміни змінної, давайте введемо нову змінну, наприклад, позначимо її як u. Заміна полягає в тому, щоб виразити x через u, що дозволить нам перетворити початкове рівняння на рівняння з однією змінною.
Проведемо заміну:
u = x²
Тоді можемо записати:
u² = (x²)² = x⁴
Тепер перепишемо початкове рівняння з використанням нової змінної:
2u² + 3u + 1 = 0
Отримане рівняння має ступінь 2, тому ми можемо застосувати звичайні методи для розв'язання квадратних рівнянь.
Для зручності позначимо коефіцієнти:
a = 2
b = 3
c = 1
Використовуючи квадратне рівняння, ми можемо використати формулу дискримінанту:
D = b² - 4ac
D = (3)² - 4(2)(1) = 9 - 8 = 1
Дискримінант D дорівнює 1.
Застосуємо формули для знаходження коренів квадратного рівняння:
x₁,₂ = (-b ± √D) / (2a)
x₁,₂ = (-3 ± √1) / (2 * 2)
x₁,₂ = (-3 ± 1) / 4
Отримуємо два розв'язки:
x₁ = (-3 + 1) / 4 = -2 / 4 = -1/2
x₂ = (-3 - 1) / 4 = -4 / 4 = -1
Отже, розв'язками початкового рівняння 2x⁴ + 3x² + 1 = 0 є x = -1/2 та x = -1.
Объяснение: