Даны последовательные члены геометрической прогрессии
b₁ = 3x - 2; b₂ = x+2; b₃ = x+8
По свойству членов геометрической прогрессии
b₂² = b₁*b₃
(x + 2)² = (3x - 2)(x + 8)
x² + 4x + 4 = 3x² + 24x - 2x - 16
x² - 3x² + 4x - 22x + 4 + 16 = 0
-2x² - 18x + 20 = 0 | : (-2)
x² + 9x - 10 = 0
Корни по теореме, обратной т. Виета
(x + 10)(x - 1) = 0
x₁ = -10; x₂ = 1
1) b₁ = 3x-2 = 3*(-10)-2 = -32;
b₂ = x+2 = -10 + 2 = -8;
b₃ = x+8 = -10 + 8 = -2
Проверка:
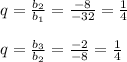
-32; -8; -2; - геометрическая прогрессия со знаменателем q=1/4
2) b₁ = 3x-2 = 3*1-2 = 1;
b₂ = x+2 = 1 + 2 = 3;
b₃ = x+8 = 1 + 8 = 9
Проверка:
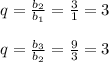
1; 3; 9; - геометрическая прогрессия со знаменателем q=3
ответ: при x₁ = -10; x₂ = 1
1.
(x+7)(x-2)=x² - 2x+7x - 14=x²+5x-14
(y+5)(y²-3y+8)=y³-3y²+8y+5y²-15y+40=y³+2y² - 7y+40
(4c-d)(6c+3d)=24c²+12cd-6cd-3d²=24c²+6cd-3d²
2.
y(a-b)+2(a-b)=(a-b)(y+2)
3x-3y+ax-ay=3(x-y)+a(x-y)=(x-y)(3+a)
3.
xy(x+y)-(x²+y²)(x-2y)=x²y+xy² - (x³-2x²y+xy²-2y³)=x²y+xy²- x³+2x²y-xy²+2y³=2y³+3x²y - x³
4.
a(a-2)-8=(a+2)(a-4)
a²-2a-8=a²-2a-8
0=0 - верно
5.
х дм - ширина прямоугольника
х+12 (дм) - длина
х+12+3 (дм) - увеличенная длина
х+2 (дм) - увеличенная ширина
х(х+12)=(х+12+3)(х+2)-80
х²+12х=х²+17х+30-80
17х-12х=50
5х=50
х=10(дм) - ширина прямоугольника
10+12=22(дм) - длина