4. 2.8ˣ⁺³ˣбольше 1, у=2.8ˣ возрастающая, поэтому х+3х больше о, т.е. 4х больше нуля, х больше нуля, т.к. 1=2⁰
8. Т.к. диагональ прямоугольника, лежащего в основании -это проекция диагонали параллелепипеда, то угол наклона диагонали к плоскости основания = углу между диагональю параллелограмма и ее проекцией, и он равен 45°, значит, высота параллелепипеда равна диагонали основания, которая находится по теореме ПИфагора √(12²+5²)=
√169=13/см/, а площадь полной поверхности равна 2*12*5+2*(12+5)*13=
120+442=562/см²/, это 2 площади основания плюс площадь боковой поверхности
6. найдем пределы интегрирования. решив уравнение х²-2х-3=0, по теореме, обратной теор. Виета, корни уравнения 3 и -1. площадь фигуры найдем как определенный интеграл от (0-(х²-2х-3))дх в пределах от -1 до 3.он равен -х³/3+х²+3х. Подставим верхний и нижний пределы предел интегрирования. -3³/3+3²+9-(1/3+1-3)=9+1 целая 2/3=10 целых 2/3 /ед.кв/.
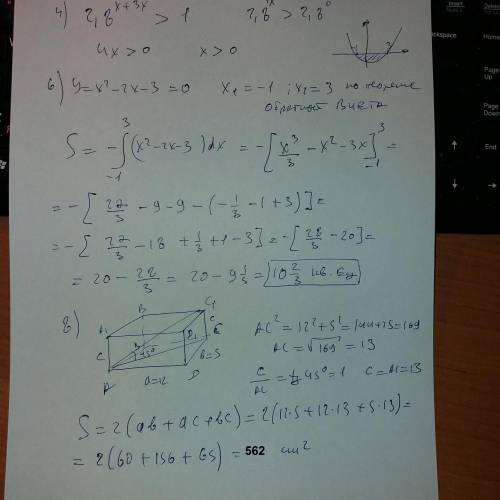
㏒₂х+㏒₂у=2; ху=2²=4, х и у положительны
2в степени (х-у)=(1/4)⁻¹,⁵
1/4 в степени -1.5=3, если равны основания, то равны и показатели степени. поэтому
х-у=3
ху=4, х=у+3, подставим во второе уравнение. у*(у+3)=4, у²+3у-4=0, по теореме, обратной теореме Виета у=1, у=-4 - не подходит, т.к. не попадает в ОДЗ, значит, у=1, тогда х=1+3=4
ответ (4;1)
9. Дана правильная четырехугольная пирамида, значит, основание высоты- точка пересечения диагоналей квадрата, который лежит в основании пирамиды и половина диагонали находим по теореме ПИфагора, т.е. как √(5²-3²)=4/м/. Тогда диагональ равна 2*4=8/м/.
Найдем площадь основания по формуле д²/2=8²/2=32/м²/. Объем пирамиды ищем по формуле v=sосн.h/3=32*3/3=32/м³/
10.Треугольник, образованный образующими конуса равнобедренный, в нем высота, проведенная к основанию, (которое являеся диаметром круга, лежащего в основании конуса), является и биссектрисой, и медианой. Раз биссектрисой, то высота лежит треугольника - осевого сечения конуса- равна половине образующей, т.е. 6см, (т.к. сумма острых углов в прямоугольном треугольнике равна 90град., и тогда высота лежит против угла в 30 град.) радиус основания конуса равен произведению образующей на косинус угла в 30 град., т.е.
12*√3/2=6√3/см/, а объем конуса v=ПR²h/3=П6²*3*6/3=216П/см³/