Общий вид линейной функции у=kх+l
а) у=2х - з - линейная, где k=2, l=-3
б) у=7-9 - частный случай линейной функции - постоянная у=2 (у=l)
Т.е. обе функции можно назвать линейными, только б) имеет своё название
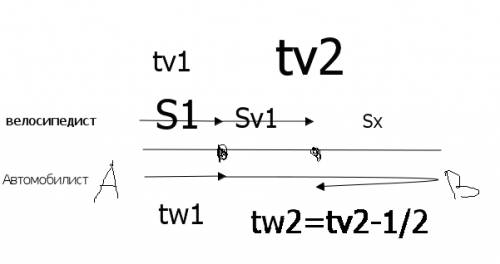
Cоставим чертёж движения смотри рис 1
пусть
15 минут = 1/4 часа
30 минут = 1/2 часа
v= скорость велосипедиста
w= скорость автомобиля
s= расстояние между АБ
s1= растояние при первой встречи от А до точки встречи 1
sv2= расстояние от первой до второй встречи для велосипедиста
sw2=расстояние от первой до второй встречи для автомобилиста
sx = расстояние которое не успел доехать велосипедист до пункта B при второй встрече
tv1=время с начала движения велосипедиста до первой встречи
tv2=время от первой встречи до второй встречи
tw1=время автомобилиста в пути (без остановки с начала движения автомобиля до первой встречи
tw2=время автомобилиста в пути (без остановки с первой встречи до второй встречи
ПЕРВЫЙ УЧАСТОК ПУТИ
s1=8+1/3 км
tw1=tv1-1/4
tv1= s1/v= 5/12 h
tw1=5/12-1/4=1/6 h
расстояние одинаковое преодолели до первой встречи и велосепедист и автомобилист значит найдём скорость автомобилиста (которая постоянна на всём участке пути )
w=s1/tw1=(25/3)/(1/6)=50
ВТОРОЙ УЧАСТОК ПУТИ
начнём с фиксации времени
tv2
tw2=tv2-1/2
теперь путь
sv1
sw2=sv1+sx*2
теперь скорости
v=20
w=50
теперь строим систему уравнений согласно формуле равномерного движения
sv1=v*tv2
sw2=w*tw2
sw2 заменим на sv1+sx*2 а также tw2 на tv2-1/2
получаем
sv1=v*tv2
sv1+sx*2=w*tv2-1/2 это уравнение равносильно (sv1) = (w)*(tv2)-(1/2) -(sx)*2
приравняем и упрастим
(w)*(tv2)-(1/2) -(sx)*2 = v*tv2 выразим sx через остальные переменные
смотри рис 2
sx=37/2
sv1=25
s1=25/3
s=s1+sv1+sx=37/2+25+25/3=51+5/6 км