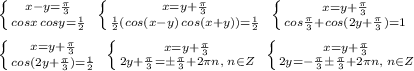
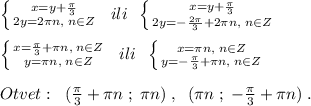
1) x² + 6x – a > 0
y = x² + 6x – a -- парабола, ветви направлены вверх (коэффициент при x² положительный). Условие x² + 6x – a > 0 означает, что парабола не пересекает ось OX, то есть уравнение y = x² + 6x – a не имеет действительных корней, что соответствует отрицательному значению дискриминанта.
D = 6² + 4a = 36 + 4a < 0
a < –9
ответ: неравенство x² + 6x – a > 0 выполняется для всех x при a < –9.
2) –x² – 7x + 2 – a < 0
y = –x² – 7x + 2 – a -- парабола, ветви направлены вниз (коэффициент при x² отрицательный). Условие –x² – 7x + 2 – a < 0 означает, что парабола не пересекает ось OX, то есть уравнение y = –x² – 7x + 2 – a не имеет действительных корней, что соответствует отрицательному значению дискриминанта.
D = (–7)² + 4(2 – a) = 57 – 4a < 0
a > 57/4
ответ: неравенство –x² – 7x + 2 – a < 0 выполняется для всех x при a > 57/4.
3) (a – 1)x² + ax + a + 2 ≤ 0
Чтобы (a – 1)x² + ax + a + 2 ≤ 0 могло выполняться при всех x, уравнение y = (a – 1)x² + ax + a + 2 должно задавать параболу, причем ее ветви должны быть направлены вниз, т.е. a – 1 < 0 ⇔ a < 1 (запомним это). Кроме того, парабола не должна пересекать ось OX, но может касаться ее, что соответствует отрицательному или нулевому значению дискриминанта.
D = a² – 4(a – 1)(a + 2) = –3a² – 4a + 8 ≤ 0
Решим квадратное уравнение –3a² – 4a + 8 = 0
D₁ = (–4)² + 4·3·8 = 112
a₁ = (4 – √112) / (–6) = (–2 + 2√7) / 3
a₂ = (4 + √112) / (–6) = (–2 – 2√7) / 3
Уравнение y = –3x² – 4x + 8 -- парабола, ветви направлены вниз, поэтому неравенство –3a² – 4a + 8 ≤ 0 верно при a ≤ (–2 – 2√7) / 3 или a ≥ (–2 + 2√7) / 3.
Совмещая это с ограничением a < 1, полученным в начале решения, имеем: a ≤ (–2 – 2√7) / 3.
ответ: неравенство (a – 1)x² + ax + a + 2 ≤ 0 выполняется для всех x при a ≤ (–2 – 2√7) / 3.